Assignment Problems

By -

Assignment Problems

A production supervisor is considering how he should assign the four jobs that are to be performed, to the four of the workers. He wants to assign the jobs to the workers such that aggregate time to perform the jobs is the least. Based on the previous experience, he has the information on the time taken by the four workers in performing these jobs, as given in the table:

image

There are four method of solving assigning problems:

(a) Complete enumeration method

(b) Transportation method

(c) Simplex method

(d) Hungarian Assignment Method

(a) Complete enumeration method

image

(c) Simplex Method:

(d) Hungarian Assignment Method

image

Hungarian Assignment Method

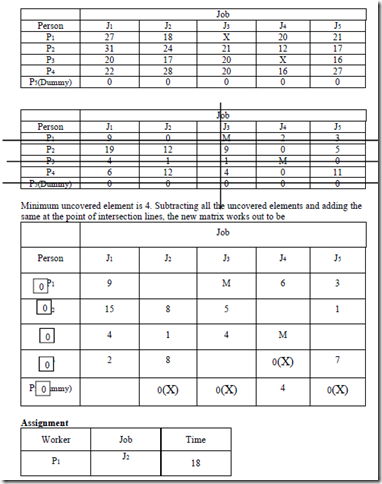
Step 1: Locate the smallest cost element in each row of the cost table. Now subtract this smallest element from each element in that row. As a result, there shall be at least one zero in each row of this new table called the reduced cost table.

Step 2: In the reduced cost table obtained, consider each column and locate the smallest element in it. Subtract the smallest value from every other entry in the column. As a consequence of this action, there would be at least one zero in each of the rows and the columns in the second reduced cost table.

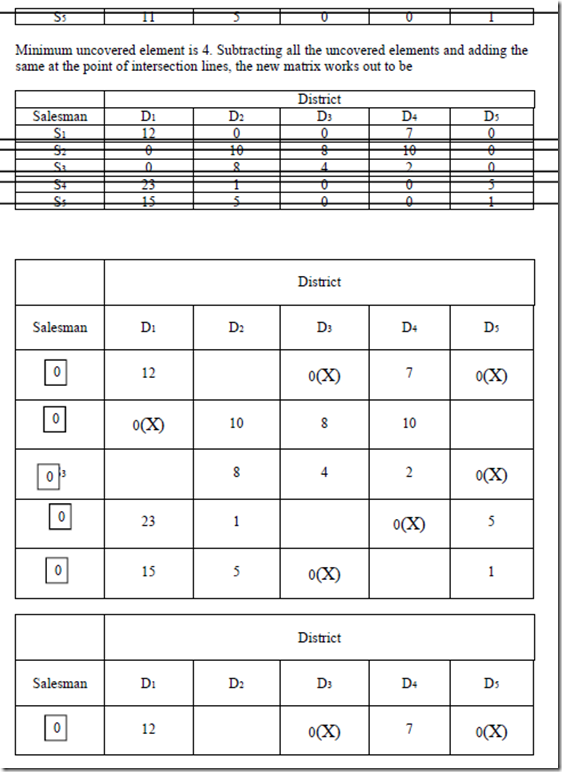
Step 3: Draw minimum number of horizontal lines and vertical lines (not the diagonal one) that are required to cover the “Zero” elements. If the number of lines drawn is equal to n (the number of rows/columns) the solution is optimal, and proceed to the step 6. If the number of lines drawn is smaller than n, go to step 4.

Step 4: Select the smallest uncovered (by the lines) cost element. Subtract this element from all uncovered elements including it and add this element to each value located at the intersection of any two lines. The cost elements through which only one line passes remain unaltered.

Step 5: Repeat steps 3 and 4 until an optimal solution is obtained.

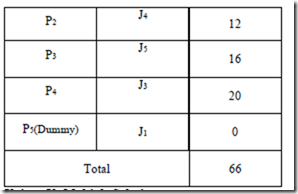
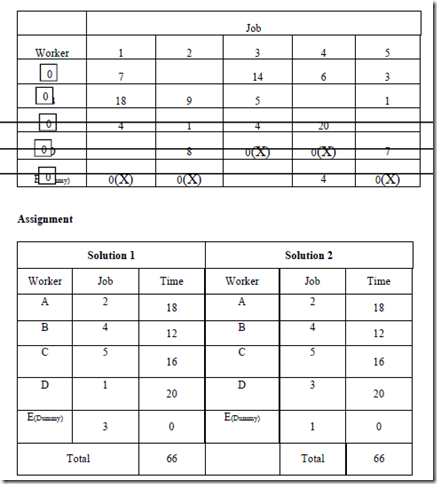
Step 6: Given the optimal solution, make the job assignments as indicated by the zero elements. This is done as follows.

a. Locate a row which contains only one zero element. Assign the job corresponding to this element to its corresponding person. Cross out the zeros, if any, in the column corresponding to the element, which is indicative of the fact that the particular job and the person is no more available.

b. Repeat (a) for each of such rows which contain only one zero. Similarly, perform the same operation in respect of each column containing only one zero element, crossing out the zero(s), if any, in the row in which the element lies.

c. If there is no row or column with only a single zero element left, then select a row/column arbitrarily and choose one of the jobs (persons) and make the assignment. Now cross the remaining zeros in the column and row in respect of which the assignment is made.

d. Repeat steps (a) through (c) until all assignments are made.

e. Determine the total cost with reference to the original cost table.

image

image

Unbalanced and Assignment

You are given the information about the cost of performing different jobs by different persons. The job-person marking X indicates that the individual involved cannot perform the particular job. Using this information, state (i) optimal assignment of jobs (ii) the cost of such assignments.

image

image

image

Unique Vs Multiple Solutions

Solve the following assignment problem and obtain the minimum cost at which all the jobs can be optimized.

image

image

Maximization Case

A company plans to assign 5 salesmen to 5 districts in which it operates. Estimates of sales revenue in thousands of rupees for each salesman in different districts are given in the following table. In your opinion, what should be the placement of the salesmen if the objective is to maximize the expected sales revenue?

image

image

Covert the given maximization problem into minimization problem by subtracting all the elements from the highest value of the element of the matrix i.e. 41. Then the minimization matrix will be

image

image

image

REFERENCES:

1. Operations Research: Theory and Applications - Sharma J. K, 4/e , Macmilan, 2010

2. Operations Research - Vohra N. D, 4/e, TMH, 2010.

3. Operations Research – Kalavathy S, 3/e, Vikas Publishing House.

4. Operations Research – Anand Sharma, HPH.

Comments

Post a Comment

Popular posts from this blog

NETWORK OPTIMIZATION MODELS:THE MINIMUM SPANNING TREE PROBLEM

By -
Image
THE MINIMUM SPANNING TREE PROBLEM The minimum spanning tree problem bears some similarities to the main version of the shortest-path problem presented in the preceding section. In both cases, an undi r ecte d and connected network is being considered, where the given information includes some mea- sure of the positive length (distance, cost, time, etc.) associated with each link. Both problems also involve choosing a set of links that have the shortest total length among all sets of links that satisfy a certain property. For the shortest-path problem, this property is that the chosen links must provide a path between the origin and the destination. For the minimum spanning tree problem, the required property is that the chosen links must provide a path between ea c h pair of nodes. The minimum spanning tree problem can be summarized as follows: 1. You are given the nodes of a network but not the links. Instead, you are given the po- tential links and the positive length for each
Read more

DUALITY THEORY:THE ESSENCE OF DUALITY THEORY

By -
Image
THE ESSENCE OF DUALITY THEORY Given our standard form for the primal problem at the left (perhaps after conversion from another form), its dual problem has the form shown to the right. Thus, with the primal problem in maximizatio n form, the dual problem is in minimization form instead. Furthermore, the dual problem uses exactly the same pa r amete r s as the primal problem, but in different locations, as summarized below. 1. The coefficients in the objective function of the primal problem are the right-hand sides of the functional constraints in the dual problem. 2. The right-hand sides of the functional constraints in the primal problem are the coef- ficients in the objective function of the dual problem. 3. The coefficients of a variable in the functional constraints of the primal problem are the coefficients in a functional constraint of the dual problem. To highlight the comparison, now look at these same two problems in matrix notation (as introduced at the beginn
Read more

DECISION SUPPORT SYSTEMS:DIALOG GENERATION AND MANAGEMENT SYSTEMS

By -
Image
DIALOG GENERATION AND MANAGEMENT SYSTEMS In our efforts in this chapter, we envision a basic DSS structure of the form shown in Figure 12. This figure also shows many of the operational functions of the database management system (DBMS) and the model base management system (MBMS). The primary purpose of the dialog generation and management system (DGMS) is to enhance the propensity and ability of the system user to use and benefit from the DSS. There are doubtless few users of a DSS who use it because of necessity. Most uses of a DSS are optional, and the decision maker must have some motivation and desire to use a DSS or it will likely remain unused. DSS use can occur in a variety of ways. In all uses of a DGMS, it is the DGMS that the user interacts with. In an early seminal text, Bennett (1983) posed three questions to indicate this centrality: 1. What presentations is the user able to see at the DSS display terminal? 2. What must the user know about what is seen at the display
Read more