QUEUEING THEORY
A flow of customers form finite\infinite population towards the service facilities form the queue (waiting line) on account of lack of capability to serve them all at a time. In the absence of a perfect balance between the service facilities and the customers, waiting time is required either for the service facilities or for the customer’s arrival.
The arriving unit that requires some service to be performed is called customer. The customer may be person, vehicles, machines, etc. Queue stands for the number of customer’s waiting to be serviced. This does not include the customer being serviced. The process or system that performs services to the customers is termed by service channel or service facility.
QUEUEING SYSTEM
A queuing system can be completely described by
(i) The input (arrival pattern)
(ii) The service mechanism)
(iii) The queue discipline, and
(iv) Customer’s behavior.
THE INPUT (ARRIVAL PATTERN)
The input describes the way in which the customer’s arrived and joins the system. Generally, customers arrive in a more or less random fashion which is not worth making the prediction. Thus the arrival pattern can be described in terms of probabilities, and consequently the probability distribution for inter-arrival times must be defined. We deal with those queuing system in which the customers arrive in Poisson fashion. The mean arrival rate is denoted by .
THE SERVICE MACHANISM
This means the arrangement of service facility to serve customers. If there is infinite number of
servers then all the customers are served instantaneously on arrival and there will be no queue. If the number of servers is finite then the customers are served according to a specific order with service time a constant or a random variable. Distribution of service time which is important in practice is the negative exponential distribution. The mean service rate is denoted by µ.
THE QUEUE DISIPLINE
It is a rule according to which the customers are selected for service when a queue has been formed. The most common disciplines are
- First come first served (FCFS)
- First in first out (FIFO)
- Last in first out (LIFO)
- Selection for service in random order (SIRO).
CUSTOMER’S BEHAVIOUR
The customers generally behave in the following four ways:
(i) Balking:
A customer who leaves the queue because the queue is too long and he has no time to wait or has no sufficient waiting space.
(ii) Reneging:
This occurs when a waiting customer leaves the queue due to impatience.
(iii) Priorities:
In certain applications some customers are served before others regardless of their arrival. These customers have priority over others.
(iv) Jockeying:
Customers may jockey from one waiting line to another. This is most common in a supermarket.
BASIC POISEN-EXPONENTIAL MODEL SINGLE SERVER
Notation (M/M/1, FCFS/).
Measuring parameters
Arrival rate is assumed to be random and hence described by Poisson distribution. It is denoted by. Service rate is to follow negative exponential distribution and is denoted by .
This is popularly used model due to its wide applicability in life. Similarly relationship for the other models can write based on assumption or arrival and service patterns.
1) The tools in a factory are issued to workmen at a centrally located tool crib. Workers who need tools are who wish to return tools approach this window where crib clerk issues or accepts tools on the basis of FCFS. The service time to receive and issue of tools is distributed negative exponentially with a mean of 4mins per workman. If workers arrive singly and at random at an average rate of 20 workers per 60 mins. Determine a) average no. Of workers waiting at the tool crib for service b) Average waiting time in the queue c) percentage time the crib clerk is idle.
2) A typist at an office receives, on an average 22 letters per day of typing. The typist works 8 hours a day and it takes on an average 20 mins to type a letter. i) What is the typist’s utilization rate? ii) What is the average numbers of letters waiting to be typed? iii) What is the average waiting time needed to have a letter typed?
3) A machine shop seeks for a contract service for repairing their “Gear hobbing machines”. The service provider has 2 repairman, one is experienced and fast and the other one is little less experienced and slow in his work. The first repairman is provided at the rate of 50/- per hour. The former can repair 7 machines per hour while the later can repair 6 machines per hour. The gear hobbing machine breakdown at the rate of 4 per hour and found to follow Poisson
distribution pattern. The cost of non-productive machine time is Rs.90/- per hour. If you are the CEO of this company on whom (out of the two) you will decide to hire??
4.) At a petrol pump, customers arrive according to a Poisson process with an average time of 5 minutes between arrivals. The service time is exponentially distributed with mean time = 2minutes. Find out the Following: i) Average queue length ii) Average number of customers in the queuing system iii) Average time spent by the car in the petrol pump iv) Average time wasted by a car before receiving petrol. What is the queuing model?
5) The arrivals at an ATM booth are assumed to be exponentially distributed. The arrival 4 per hour and the service rate is 12 per hour. Determine: i) Average number of customers in the system ii) Average number of customer waiting to be served or average queue length iii) Average time a customer spends system iv) Average waiting time of a customer before being served.
6) A self service stores employee’s one cashier at its corner. Nine customers arrive on an average every 5 minutes while cashier can serve 10 customers in 5 minutes. Assuming Poisson distribution for arrival rate and exponential distribution for service rate, find i) Average number of customers in the system ii) Average time a customer spends in the system iii) Average queue length.
7) The Taj service station has a central store where service mechanics arrive to take spare parts for the job they work upon. The mechanics wait in queue if necessary and are served on FIFO basis. The store is manned by attendant who can attend 8 mechanics in an hour on an average. The arrival rate of mechanics arrivals in Poisson distributed and service exponentially distributed, determine Ws, Wq, and Lq where their symbol carry their usual meaning.
8) A person repairing radios find that the time spent on the radio sets has an exponential distribution with mean 20 minutes. If the radios in the order in which they come in and their arrival is approximately Poisson with an average rate of 15 for 8 hour day, what is the repairman’s expected idle time each day? How many jobs are ahead of the average set just brought in?
9) A branch of a bank has only one typist. Since the typing work varies in length, the typing rate is randomly distributed approximately a Poisson distribution with mean strike rate of 8 letters per hour. The letters arrive at a rate of 5 per hour during the entire 8 hour workday. If the typewriter is valued at Rs.15 per hour. Determine i) Equipment utilization ii) Average idle time cost of the typewriter per day iii) Average system time.
10) At Dr Prachi’s clinic, on an average 6 patients arrive per hour. The clinic is attended by Prachi herself. Some patients require only the repeat prescription; others come for check up, while some others require a thorough inspection for the diagnosis. This takes the doctor 6 minutes per patient on an average. It can be assumed that arrivals follow Poisson distribution and the doctor’s inspection time follows an exponential distribution. Determine i) percent of times a patient can walk right inside doctor’s cabin without having to wait. ii) The average number of patients waiting for their turn iv) the average time a patient spends in the clinic.
11) A belt snapping for conveyor’s in an open cast mine occur at the rate of 2 per shift. There is only one hot plate available for vulcanizing and it can vulcanize on a average 5 belts snap/ shift.
i) What is the probability that when a belt snaps, the hot plate is readily available? ii) What is the average number of belts in the system? iii) What is the waiting time of an arrival? iv) What is the average waiting time plus vulcanizing time?
12) On an average 96 patients per 24 hour day require the service of a clinic. A patient on an average requires 10 minutes of attention. Clinic can handle only one emergency at a time. It co sts the clinic Rs.100 per patient treated to serve in 10minutes and each minute of decrease in average time costs Rs. 10 per patient treated. How much should be budgeted to reduce average size of queue to 0.5 patients?
If the length of the queue should be 0.5 then the service time must be reduced to 7.5. The decrease in the service time is 2.5 minutes.
Therefore, the increase in the cost is Rs.25 and hence the budgeted cost should be 100+25 = Rs.125.





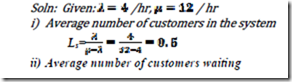


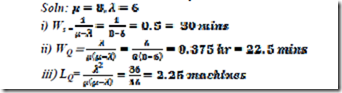









Comments
Post a Comment