Structure of the Transportation Problem

By -

Introduction

Ah… finally after 14 weeks…my favorite of all quantitative method applications… the transportation problem. For seventeen years in the Air Force, most of my career was spent figuring out how to efficiently move troops and their equipment, weapons and weapon systems, communication equipment, and medical supplies from point A to point

B. Then, when I moved to the Pentagon to finish my career as Chief of Air Force Transportation Programs, I worked for three years on how to effectively deploy troops and their equipment, weapons and weapon systems, communication equipment, and medical suppliers from many ports of embarkation to multiple ports of debarkation.

After I retired from the Air Force and joined the faculty at the University of South Florida, my initial applied research was working with supply chain managers at Johnson & Johnson and 3M to figure out how to effectively move J&J medical products and 3M consumer products through their supply chains. For 3M, this included using quantitative methods to help decide where intermediate distribution centers should be located, especially to meet European expansion in the early 1990's.

Whether in military or commercial applications, the transportation problem is that problem which addresses what origin point should ship to what final destination point over which route so as to minimize transportation costs while meeting the problem constraints. The problem constraints are staying within the available supply at the origins, and meeting customer demand at the destinations.

The problem can become quickly complex by adding intermediate transshipment points, such as distribution centers, which add constraints such as whatever is shipped

clip_image010_thumbinto transshipment points must be shipped out. The transshipment problem is the subject of Module 7.2 Notes. Complexity is also added by placing capacity constraints on the routes or the transshipment points.

You will see that the transportation problem is simply another application of linear programming, but it is such a widespread application that this and other quantitative texts devote a chapter just to this application. Companies like 3M that have multiple manufacturing sites, many distribution centers and warehouses, and multiple consumer demand locations find the transportation problem to be so complex that linear programming applications are in common use.

Illustration of the General Transportation Problem

Let's start this module with a simplified example of the problem facing logistics staffs at the Pentagon. How many troops should be deployed from aerial and water ports of embarkation to aerial and water ports of debarkation so as to minimize total deployment time. For example, we could use Fort Bragg, North Carolina and Fort Hood, Texas as aerial ports of embarkation and Adana, Turkey; Dhahran, Saudi Arabia; and Wheelus, Libya as aerial ports of debarkation. Please understand that this is not an actual deployment scenario; but rather an example for illustration.

The constraints include "supply" and "demand." Supply constraints are used to ensure that the number of troops deployed do not exceed the number available at the two ports of embarkation. Demand constraints are used to ensure that the number of troops deployed meet the need for troops at the ports of debarkation.

Before continuing, please understand that the two origins could be Detroit and Memphis automobile production plants. The three destinations could be customers (automobile dealerships) in Philadelphia, Washington DC and Miami. Instead of moving 20,000 troops, we may be moving 20,000 new cars out of Detroit and Memphis to meet dealer demand at the three destinations.

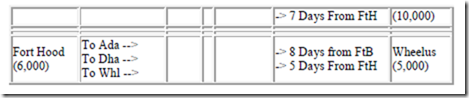
The following table presents a picture of this transportation problem. The table includes the nodes (origins and destinations) and the arcs (deployment or shipping routes).

image

image

clip_image010[1]_thumbThe table shows that 14,000 troops are available for deployment out of Fort Bragg. It takes 7 days to deploy troops from Fort Bragg to Adana, which has a demand for 5,000 troops. So, one alternative is to deploy 5,000 troops out of Fort Bragg to Adana, leaving 9,000 troops available at Fort Bragg for Dhahran or Wheelus. The "cost" of this move would be 5,000 troops times 7 days giving 35,000 troop deployment days.

Another way of satisfying the demand at Adana is to deploy 5,000 troops from Fort Hood. Note it takes 10 days to deploy troops from Fort Hood to Adana, which would give 5,000 times 10 days or 50,000 troop deployment days. We could continue to try different combinations of origins and destinations to minimize total troop deployment days while meeting demand and staying within troop availability constraints. For a small problem, it would not be too difficult to try all of the combinations of solutions to find the optimal solution. But if there were many origins, such as 10 or more, and many destinations, such as 15 or more, the problem would be too cumbersome to work "by hand."

I should note here that in the parallel automobile example, the 7, 10 and other deployment day coefficients might be $700, $1000 and other freight charges. The objective for the commercial application would be to minimize transportation costs while meeting demand and staying within the available supply constraints.

Linear programming is an excellent quantitative method for application to the transportation problem. Recall from Module 6, that to formulate a linear program we need to decide on the decision variables, create the objective function as a linear equation, and then formulate the constraints as linear equations.

For the transportation problem, the decision variables are: FtB_Ada = Nbr of troops to deploy from Fort Bragg to Adana

FtB_Dha = Nbr of troops to deploy from Fort Bragg to Dhahran

FtB_Whl = Nbr of troops to deploy from Fort Bragg to Wheelus

FtH_Ada = Nbr of troops to deploy from Fort Hood to Adana

FtH_Dha = Nbr of troops to deploy from Fort Hood to Dhahran

FtH_Whl = Nbr of troops to deploy from Fort Hood to Wheelus

Note that the number of variables for the standard transportation problem is the number of origins times the number of destinations. For this problem, there are two origins and three destinations which gives 2 times 3 or 6 decision variables. The decision variables then represent the units shipped over the deployment or shipping routes. Also note that I used a code for naming the variables. The text uses X12 to represent the number of

units shipped from origin one to destination 2. I like to use a more descriptive code to represent the route, and abbreviate names to keep within the 8 character variable name restrictions of The Management Scientist.

The objective function is to minimize troop deployment days, where days ("costs") are the coefficients multiplied times the number of troops routing decision variables.

Minimize Z = 7 FtB_Ada + 8 FtB_Dha + 8 FtB_Whl

+10 FtH_Ada + 7 FtH_Dha + 5 FtH_Whl

To show how this equation works, let's compute the deployment days for the solution FtB_Ada = 5,000; FtB_Dha = 5,000; Fth_Whl = 4,000; Fth_Dha = 5,000 and FtH_Whl = 1,000.

Minimize Z = 7 (5,000) + 8 (5,000) + 8 (4,000) + 7 (5,000)

+ 5 (1,000) = 147,000 troop deployment days

This is a feasible solution but we do not know if it is optimal until we try all combinations (or finish the constraint set and let the computer software run the combinations). Now for the constraints which include staying within the available supply at each origin node.

Fort Bragg Supply: FtB_Ada + FtB_Dha + FtB_Whl < 14,000

Fort Hood Supply: FtH_Ada + FtH_Dha + FtH_Whl < 6,000

The constraints also include meeting the customer demand:

Adana Demand: FtB_Ada + FtH_Ada = 5,000

Dhahran Demand: FtB_Dha + FtH_Dha = 10,000

Wheelus Demand: FtB_Whl + FbH_Whl = 5,000

Note that I made the demand constraints strict equalities, but allowed for slack in the supply constraints. This general formulation works as long as supply = demand or supply is greater than demand. If supply is greater than demand, the slack constraint will indicate which origin should have the excess supply. I will talk about how to handle the special case of demand being greater than supply after we look at the solution.

Comments

Post a Comment

Popular posts from this blog

DUALITY THEORY:THE ESSENCE OF DUALITY THEORY

By -
Image
THE ESSENCE OF DUALITY THEORY Given our standard form for the primal problem at the left (perhaps after conversion from another form), its dual problem has the form shown to the right. Thus, with the primal problem in maximizatio n form, the dual problem is in minimization form instead. Furthermore, the dual problem uses exactly the same pa r amete r s as the primal problem, but in different locations, as summarized below. 1. The coefficients in the objective function of the primal problem are the right-hand sides of the functional constraints in the dual problem. 2. The right-hand sides of the functional constraints in the primal problem are the coef- ficients in the objective function of the dual problem. 3. The coefficients of a variable in the functional constraints of the primal problem are the coefficients in a functional constraint of the dual problem. To highlight the comparison, now look at these same two problems in matrix notation (as introduced at the beginn...
Read more

NETWORK OPTIMIZATION MODELS:THE MINIMUM SPANNING TREE PROBLEM

By -
Image
THE MINIMUM SPANNING TREE PROBLEM The minimum spanning tree problem bears some similarities to the main version of the shortest-path problem presented in the preceding section. In both cases, an undi r ecte d and connected network is being considered, where the given information includes some mea- sure of the positive length (distance, cost, time, etc.) associated with each link. Both problems also involve choosing a set of links that have the shortest total length among all sets of links that satisfy a certain property. For the shortest-path problem, this property is that the chosen links must provide a path between the origin and the destination. For the minimum spanning tree problem, the required property is that the chosen links must provide a path between ea c h pair of nodes. The minimum spanning tree problem can be summarized as follows: 1. You are given the nodes of a network but not the links. Instead, you are given the po- tential links and the positive length for each ...
Read more

INTEGER PROGRAMMING:THE BRANCH-AND-CUT APPROACH TO SOLVING BIP PROBLEMS

By -
TH E BRANCH-AND-CUT APPROACH TO SOLVING BIP PROBLEMS Integer programming has been an especially exciting area of OR since the mid-1980s be- cause of the dramatic progress being made in its solution methodology. Background To place this progress into perspective, consider the historical background. One big break- through had come in the 1960s and early 1970s with the development and refinement of the branch-and-bound approach. But then the state of the art seemed to hit a plateau. Rel- atively small problems (well under 100 variables) could be solved very efficiently, but even a modest increase in problem size might cause an explosion in computation time be- yond feasible limits. Little progress was being made in overcoming this exponential growth in computation time as the problem size was increased. Many important problems arising in practice could not be solved. Then came the next breakthrough in the mid-1980s, with the introduction of the b r an c h- and-cu t approach to sol...
Read more