Transportation problem

Transportation problem

Operations research (OR) are concerned with scientifically deciding how to best design and operate people–machine systems, usually under conditions requiring the allocation of scarce

resources . (1Operations Research Society of America).

Operations research tools and has been a decision-making aid in almost all manufacturing industries and in financial and service organizations. Key problem managers face is how to allocate scarce resources among various activities or projects. Linear programming, or LP, is a method of allocating resources in an optimal way. It is one of the most widely used In the term linear programming, programming refers to mathematical programming.

One of the most important and successful applications of quantitative analysis to solving business problems has been in the physical distribution of products, commonly referred to as transportation problems. Basically, the purpose is to minimize the cost of shipping goods from one location to another so that the needs of each arrival area are met and every shipping location operates within its capacity. However, quantitative analysis has been used for many problems other than the physical distribution of goods.

We could set up a transportation problem and solve it using the simplex method as with any LP problem (see using the Simplex Method to Solve Linear Programming Maximization

However, the special structure of the transportation problem allows us to solve it with a faster, more economical algorithm than simplex. Problems of this type, containing thousands of variables and constraints, can be solved in only a few seconds on a computer. In fact, we can solve a relatively large transportation problem by hand.

There are some requirements for placing an LP problem into the transportation problem category.

The transportation problem

Linear programming is good at solving problems with zillions of options, and finding the optimal solution. Could it work for transportation problems? Costs are linear, and shipment quantities are linear, so maybe so.

Since any transportation problem can be formulated as an LP, we can use the simplex method to find an optimal solution. Because of the special structure of a transportation LP, the iterations of the simple method have a very special form. The transportation simplex method is nothing but the original simplex method, but it streamlines the iterations given this special form.

Introduction

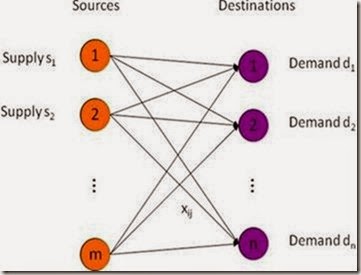
Consider a commodity which is produced at various centers called SOURCES and is demanded at various other DESTINATIONS. The production capacity of each source (availability) and the requirement of each destination are known and fixed.

The cost of transporting one unit of the commodity from each source to each destination is also known. The commodity is to be transported from various sources to different destinations in such a way that the requirement of each destination is satisfied and at the same time the total cost of transportation in minimized.

This optimum allocation of the commodity from various sources to different destinations is called TRANSPORTATION PROBLEM.

• Transportation models deals with the transportation of a product manufactured at different plants or factories (supply origins) to a number of different warehouses (demand destinations).

• The objective to satisfy the destination requirements within the plants capacity constraints at the minimum transportation cost.

A typical transportation problem contains

• Inputs:

• Sources with availability

• Destinations with requirements

• Unit cost of transportation from various sources to destinations

• Objective:

• To determine schedule of transportation to minimize total transportation cost.

Simple Network Representation

A transportation problem can be stated mathematically as follows:

Let there be ‘m’ SOURCES and ‘n’ DESTINATIONS

Let ai : the availability at the ith source

bj : the requirement of the jth destination.

Cij : the cost of transporting one unit of commodity from the ith source to the jth destination

A solution where the row total of allocations is equal to the availabilities and the column total is equal to the requirements is called a feasible solution .The solution with m+n-1 allocations is called a Basic Solution.

Prototype Problem

• Holiday shipments of iPods to distribution centers

• Production at 3 facilities,

– A, supply 200k

– B, supply 350k

– C, supply 150k

• Distribute to 4 centers,

– N, demand 60k

– S, demand 140k

– E, demand 300k

– W, demand 200k

• Total demand vs. total supply

•

• Holiday shipments of iPods to distribution centers

• Production at 3 facilities,

– A, supply 200k

– B, supply 350k

– C, supply 150k

• Distribute to 4 centers,

– N, demand 60k

– S, demand 140k

– E, demand 300k

– W, demand 200k

• Total demand vs. total supply

• Prototype Problem

When solving the transportation problem, the number of possible routes should be £

m+n-1.

If it is <m+n-1, it is called a degenerate solution.

In such a case evaluation of the solution will not be possible.

In order to evaluate the cells /routes (using the Modi-method or the stepping stone method) we need to imagine/introduce some used cells/routes carrying / transporting a very small quantity, say e. That cell should be selected at the correct place.

• Solution of transportation problems

• Two phases:

• First phase:

• Find an initial feasible solution

• 2nd phase:

• Check for optimality and improve the solution

• Find an initial feasible solution

• North west corner method

• Least cost method

• Vogel’s approximation method

• Checking for optimality

a) Stepping stone method

b) Modified distribution (MODI) method.

Steps in Solving the Transportation Problem How to solve?

1. Define the objective function to be minimized with the constraints imposed on the problem.

2. Set up a transportation table with m rows representing the sources and n columns representing the destination

3. Develop an initial feasible solution to the problem by any of these methods

4. a) The North west corner rule

5. b) Lowest cost entry method

6. c)Vogel’s approximation method

4. Examine whether the initial solution is feasible or not.( the solution is said to be feasible if the solution has allocations in ( m+n-1) cells with independent positions.

5. Test wither the solution obtained in the above step is optimum or not using

a) Stepping stone method

b) Modified distribution (MODI) method.

6. If the solution is not optimum, modify the shipping schedule. Repeat the above until an optimum solution is obtained.

• Applications

• To minimize shipping costs from factories to warehouses or from warehouses to retails outlets.

• To determine lowest cost location of a new factory, warehouse or sales office.

• To determine minimum cost production schedule that satisfies firm’s demand and

production limitations.

North-West Corner Method

Step1: Select the upper left (north-west) cell of the transportation matrix and allocate the maximum possible value to X11 which is equal to min(a1,b1).

Step2: If allocation made is equal to the supply available at the first source (a1 in first row), then move vertically down to the cell (2,1).

• If allocation made is equal to demand of the first destination (b1 in first column), then mov

• e horizontally to the cell (1,2).

• If a1=b1 , then allocate X11= a1 or b1 and move to cell (2,2).

Step3: Continue the process until an allocation is made in the south-east corner cell of the transportation table.

Advantages; it is simple and reliable. Easy to compute understand and interpret.

Disadvantages: This method does not take into considerations the shipping cost, consequently the initial solution obtained by this method require improvement.

• Problem1: Obtain initial solution in the following transportation problem by using Northwest corner rule method

Least Cost Method

Step1: Select the cell having lowest unit cost in the entire table and allocate the minimum of supply or demand values in that cell.

Problem1: Obtain initial solution in the following transportation problem by using LCM method.

Step2: Then eliminate the row or column in which supply or demand is exhausted. If both the supply and demand values are same, either of the row or column can be eliminated.

In case, the smallest unit cost is not unique, then select the cell where maximum allocation can be made.

Step3: Repeat the process with next lowest unit cost and continue until the entire available supply at various sources and demand at various destinations is satisfied.

Vogel’s Approximation Method

• Step1: Calculate penalty for each row and column by taking the difference between the two smallest unit costs. For each row and column, calculate its difference:

= (Second smallest cij in row/col) - (Smallest cij in row/col)

This penalty or extra cost has to be paid if one fails to allocate the minimum unit transportation cost.

• Step3: Adjust the supply and demand and eliminate the satisfied row or column.

Eliminate any row/column with no supply / demand left from further steps. If a row and column are satisfied simultaneously, eliminate both the row and column.

Step4:. Recompute the row and column difference for the reduced transportation table, omitting rows or columns crossed out in the preceding step.

Step5:

Repeat the process until all the supply sources and demand destinations are satisfied. Repeat until BFS found.

Repeat the above procedure until the entire supply at factories are exhausted to satisfy

demand at different warehouses.

• Problem1: Obtain initial solution in the following transportation problem by using VAM method

• Problem 2: Obtain initial solution in the following transportation problem by using VAM

Algorithm of MODIFIED DISTRIBUTION (MODI) METHOD

Step I: For an initial basic feasible solution with (m+n-1) occupied (basic) cells, calculate ui and vj values for rows and columns respectively using the relationship Cij = ui + vj for all allocated cells only. To start with assume any one of the ui or vj to be zero.

as Δij = Cij – (ui + vj). Step III:

a) If all Δij > 0, the current solution is optimal and unique.

b) If any Δij = 0, the current solution is optimal, but an alternate solution exists.

c) If any Δij < 0, then an improved solution can be obtained; by converting one of the basic cells to a non basic cells and one of the non basic cells to a basic cell. Go to step IV.

Step IV: Select the cell corresponding to most negative cell evaluation.

This cell is called the entering cell. Identify a closed path or a loop which starts and ends at the entering cell and connects some basic cells at every corner. It may be noted that right angle turns in this path are permitted.

Step V: Put a + sign in the entering cell and mark the remaining corners of the loop alternately with – and + signs, with a plus sign at the cell being evaluated.

8. Determine the maximum number of units that should be shipped to this unoccupied cell.

The smallest one with a negative position on the closed path indicates the number of units that can be shipped to the entering cell.

This quantity is added to all the cells on the path marked with plus sign and subtract from those cells mark with minus sign.

In this way the unoccupied cell under consideration becomes an occupied cell making one of the occupied cells as unoccupied cell.

9. Repeat the whole procedure until an optimum solution is attained i.e. Δij is positive or zero.

Finally calculate new transportation cost.

• Unbalanced transportation

• Restricted routes

• Maximisation

Unbalanced transportation problem

When the total availability is equal to the total requirement the problem (i.e. Σai =

Σbj) is said to be a balanced transportation problem.

If the total availability at different sources is not equal to the total requirement at different destinations, (i.e. Σai ≠ Σbj), the problem is said to be an unbalanced transportation problem.

Steps to convert an unbalanced problem to a balanced one are

1) If Σai > Σbj i.e. the total availability is greater than the total requirement, a dummy destination is introduced in the transportation problem with requirement = Σai - Σbj.

2) The unit cost of transportation from each source to this destination is assumed to

be zero.

3) If Σai < Σbj i.e. the total availability is less than the total requirement, a dummy source is introduced in the transportation problem with requirement = Σbj - Σai. The unit cost of transportation from each destination to this source is assumed to be zero.

After making the necessary modifications in the given problem to convert it to a balanced problem, it can be solved using any of the methods.

• Include a dummy source or a dummy destination having a supply “d” or demand “d” to convert it to a balanced transportation problem.

• Where d =

Problem

• .Holiday shipments of iPods to distribution centers

• Production at 3 facilities,

• A, supply 200k

• B, supply 350k

• C, supply 150k

• Distribute to 4 centers,

• N, demand 160k

• S, demand 140k

• E, demand 300k

• W, demand 200k

• Total demand ≠ total supply

• Obtain initial solution in the following transportation problem by using VAM method

Restricted routes

• Sometimes in a transpiration problem some routes may not be available.

This could be due to a variety of reasons like unfavorable weather condition or a strike on particular route etc.

• In such a situation there is a restrictions on route available for transportation.

• We assign a very large cost represented by M to each of such routes which are not available.

• The effect of adding a large cost element would be that such routes would automatically be eliminated in the final solutions.

Because of railroad construction, shipments are temporarily prohibited from warehouse at city A to company C1.i) Find the optimal distribution for XYZ tobacco Company.

Maximisation Problem

• A Transpiration Tableau contains unit profits instead of unit costs and the objective function be the maximization of profits.

• To convert maximization problem to minimization all the values of profit matrix are subtracted from the highest profit value in the matrix

• The objective function is determined with reference to the original profit matrix

• If a maximization type of transportation problem is unbalanced then it should be balanced by introducing necessary dummy row or column before converting it into maximization problem.

• Similarly if such a problem has prohibited route, then the pay of element for such a route should be submitted by –M before proceeding to convert to maximization type.