INDUSTRIAL ENGINEERING APPLICATIONS IN FINANCIAL ASSET MANAGEMENT:AN ILLUSTRATION

By -
AN ILLUSTRATION
The Efficient Frontier

To illustrate the essence of the asset-allocation problem, I begin with a simple example that includes the following assets: U.S. stocks, international stocks, U.S. bonds, international bonds, and cash. This constitutes a broad asset mix typical of that used by many professional managers. Expected returns are 11.0%, 12.6%, 6.0%, 6.9%, and 5.0%, respectively. The expected standard deviations (risk) of these returns are 12.5%, 14.7%, 4.3%, 7.8%, and 0.0%. Note that the standard deviation of cash returns is zero because this asset is presumed to consist of riskless U.S. Treasury securities. The correlation matrix for asset returns is:

Industrial Engineering Applications in Financial Asset Management-0005

Optimum portfolios are obtained by selecting the asset weights that maximize portfolio return for a specific portfolio risk. The problem constraints are that (1) the portfolio return is a linear combi- nation of the separate asset returns, (2) portfolio variance is a quadratic combination of weights, asset risks, and asset correlations, and (3) all weights are positive and sum to one.

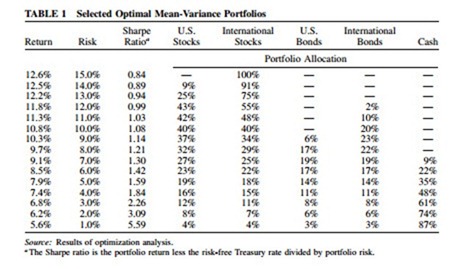
The results of producing MV portfolios are presented in Table 1. The corresponding efficient frontier is shown in Figure 1. The allocations obtained are typical for analyses of this type. That is, to obtain higher portfolio returns, the investor must take on more risk. This is accomplished by weighting equities more heavily. The most conservative portfolios have both low returns and low risk. They consist primarily of cash and bonds. For moderate levels of risk, investors should blend stocks and bonds together in more equal proportions. In addition, note that the most risky portfolios skew to higher weights for international equities, which are more risky than U.S. stocks.

It should be obvious that the production of MV portfolios is not extraordinarily input intensive. Efficient frontiers for five asset portfolios require only five predicted returns, five standard deviations, and a five-by-five symmetrical matrix of correlation coefficients. Yet the process yields indispensable information that allows investors to select suitable portfolios.

Investor Risk Preferences

Once the efficient frontier is established, the issue of investor risk preferences must be addressed. Individuals exhibit markedly different attitudes towards risk. Some are extremely risk averse, toler- ating nothing but near certainty in life. Others relish risk taking. Most are somewhere between these two extremes.

Risk attitudes depend on personality, life experience, wealth, and other socioeconomic factors. By default, extremely risk-averse investors are not interested in building wealth via asset accumu- lation, because they are unwilling to tolerate the risk necessary to obtain high returns. The opposite is true for adventurous souls ready to gamble for large payoffs. In this regard, ‘‘old-money’’ investors

Industrial Engineering Applications in Financial Asset Management-0006

are usually more risk averse than ‘‘new-money’’ investors. They require portfolios heavily weighted in conservative assets. New-money investors are comfortable with inherently risky equities (Figure 2). Age often plays an important role. Older investors are commonly more risk averse because they are either retired or close to retirement and dissaving (Figure 3).

How does one ascertain risk tolerance to guarantee a relevant portfolio is matched to the investor’s needs? There are a number of ways. One is to estimate the risk-aversion parameter based on the investor’s response to a battery of questions designed to trace out their return preferences with different payoff probabilities.

Some financial managers simply use personal knowledge of the investor to deduce risk tolerance. For example, if an investor with a $10 million portfolio is distraught if the portfolio’s value plunges 20% in a year, he or she is not a candidate for an all-equity portfolio. Yet another approach used by some managers is to work backwards and determine the risk necessary for the investor to reach specific wealth-accumulation goals.

Industrial Engineering Applications in Financial Asset Management-0007

Industrial Engineering Applications in Financial Asset Management-0008

Comments

Post a Comment

Popular posts from this blog

DUALITY THEORY:THE ESSENCE OF DUALITY THEORY

By -
Image
THE ESSENCE OF DUALITY THEORY Given our standard form for the primal problem at the left (perhaps after conversion from another form), its dual problem has the form shown to the right. Thus, with the primal problem in maximizatio n form, the dual problem is in minimization form instead. Furthermore, the dual problem uses exactly the same pa r amete r s as the primal problem, but in different locations, as summarized below. 1. The coefficients in the objective function of the primal problem are the right-hand sides of the functional constraints in the dual problem. 2. The right-hand sides of the functional constraints in the primal problem are the coef- ficients in the objective function of the dual problem. 3. The coefficients of a variable in the functional constraints of the primal problem are the coefficients in a functional constraint of the dual problem. To highlight the comparison, now look at these same two problems in matrix notation (as introduced at the beginn...
Read more

NETWORK OPTIMIZATION MODELS:THE MINIMUM SPANNING TREE PROBLEM

By -
Image
THE MINIMUM SPANNING TREE PROBLEM The minimum spanning tree problem bears some similarities to the main version of the shortest-path problem presented in the preceding section. In both cases, an undi r ecte d and connected network is being considered, where the given information includes some mea- sure of the positive length (distance, cost, time, etc.) associated with each link. Both problems also involve choosing a set of links that have the shortest total length among all sets of links that satisfy a certain property. For the shortest-path problem, this property is that the chosen links must provide a path between the origin and the destination. For the minimum spanning tree problem, the required property is that the chosen links must provide a path between ea c h pair of nodes. The minimum spanning tree problem can be summarized as follows: 1. You are given the nodes of a network but not the links. Instead, you are given the po- tential links and the positive length for each ...
Read more

INTEGER PROGRAMMING:THE BRANCH-AND-CUT APPROACH TO SOLVING BIP PROBLEMS

By -
TH E BRANCH-AND-CUT APPROACH TO SOLVING BIP PROBLEMS Integer programming has been an especially exciting area of OR since the mid-1980s be- cause of the dramatic progress being made in its solution methodology. Background To place this progress into perspective, consider the historical background. One big break- through had come in the 1960s and early 1970s with the development and refinement of the branch-and-bound approach. But then the state of the art seemed to hit a plateau. Rel- atively small problems (well under 100 variables) could be solved very efficiently, but even a modest increase in problem size might cause an explosion in computation time be- yond feasible limits. Little progress was being made in overcoming this exponential growth in computation time as the problem size was increased. Many important problems arising in practice could not be solved. Then came the next breakthrough in the mid-1980s, with the introduction of the b r an c h- and-cu t approach to sol...
Read more