EXAMPLES OF PERFORMING SIMULATIONS ON SPREADSHEETS WITH ANALYTIC SOLVER PLATFORM:DECISION MAKING WITH PARAMETER ANALYSIS REPORTS AND TREND CHARTS

By -

DECISION MAKING WITH PARAMETER ANALYSIS REPORTS AND TREND CHARTS

Many simulation models include at least one decision variable. For example, the model formulated for both the bidding example in Sec. 28.1 and the overbooking example in Sec.

28.5 included a single decision variable, as listed below:

Bidding example: OurBid (C25) in Fig. 28.2

Overbooking example: ReservationsToAccept (C13) in Fig. 28.16

In both of these cases, you have seen how well simulation with ASPE can evaluate a particular value of the decision variable by providing a wealth of output for the results cell(s). However, in contrast to many OR techniques, this approach has not identified an optimal solution for the decision variable(s). Fortunately, ASPE provides a way to systematically perform multiple simulations by using parameter cells. This makes it easy to identify at least an approximation of an optimal solution for problems with only one or two decision variables. In this section, we describe this approach and illustrate it by applying it in turn to the two decision variables listed above. (Recall that Sec. 20.6 included still another approach, using the Solver in ASPE to search for an optimal solution for simulation models.)

An intuitive approach for searching for an optimal solution is to use trial and error. Try different values of the decision variable(s), run a simulation for each, and see which one provides the best estimate of the chosen measure of performance. The interactive simulation mode in ASPE makes this especially easy, since the results in the statistic cells are available immediately after changing the value of a decision variable. Using parameter cells allows you to do the same thing in a more systematic way. After defining a parameter cell, all the desired simulations are run and the results soon are displayed nicely in the parameter analysis report. If desired, you also can view an enlightening trend chart, which can provide additional details about the results.

If you have previously used parameter cells with the Solver in ASPE to generate para- meter analysis reports for performing sensitivity analysis systematically (as was done in Chap. 7), the parameter analysis reports in simulation models work in much the same way. Two is the maximum number of decision variables that can be varied simultaneously in a parameter analysis report.

Let us begin by returning to the bidding example mentioned above and use a parame- ter cell to run multiple simulations.

A Parameter Analysis Report for the Reliable Construction Co. Bidding Problem

We turn now to generating a parameter analysis report for the Reliable Construction Co. bidding problem presented in Sec. 28.1. Since the procedure for how to generate a parameter analysis report already has been presented in Sec. 20.6, our focus here is on summarizing the results.

Recall that the management of the company is concerned with determining what bid it should submit for a project that involves constructing a new plant for a major manufacturer. Therefore, the decision variable in the spreadsheet model in Fig.28.2 is OurBid (C25). The parameter cell dialog box in Fig. 28.29 is used to further describe this decision variable. Management feels that the bid should be in the range between $4.8 million and

$5.8 million, so these are the numbers (in units of millions of dollars) that are entered into the entry boxes for Bounds in this dialog box.

INTRODUCTION TO OPERATIONS RESEARCH-0701

INTRODUCTION TO OPERATIONS RESEARCH-0702

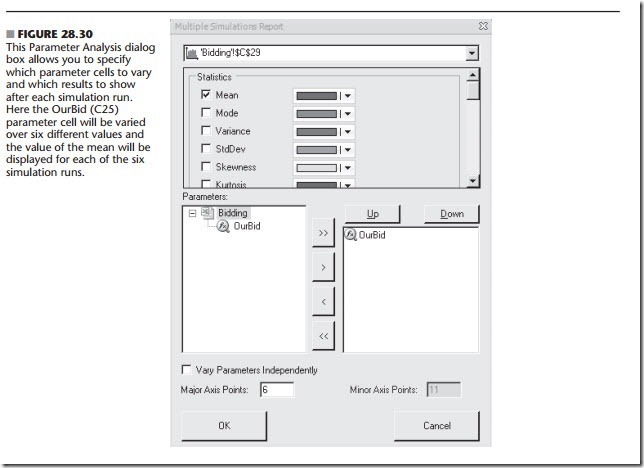
Management wants to choose the bid that would maximize its expected profit. Consequently, the results cell in the spreadsheet model is Profit (C29). After choosing Parameter Analysis from the Reports>Simulation menu on the ASPE ribbon, the corresponding dialog box in Fig. 28.30 is used to specify that the mean of the Profit should be shown as the

INTRODUCTION TO OPERATIONS RESEARCH-0703

parameter cell OurBid is varied over six major axis points. The six values automatically are distributed evenly over the range specified in Fig. 28.29, so simulations will be run for bids of 4.8, 5.0, 5.2, 5.4, 5.6, and 5.8 (in millions of dollars).

Figure 28.31 shows the resulting parameter analysis report. A bid of $5.4 million gives the largest mean value of the profits obtained on the 1,000 trials of the simulation run. This mean value of $482,000 in cell B5 should be a close estimate of the expected profit from using this bid. The prototype example in Chap. 22 begins with the company having just won the contract by submitting this bid.

Problem 28.8 asks you to refine this analysis by generating a parameter analysis report that considers all bids between $5.2 million and $5.6 million in multiples of $0.05 million.

A Parameter Analysis Report and Trend Chart for the Transcontinental Airlines Overbooking Problem As described in Sec. 28.5, Transcontinental Airlines has a popular daily flight from San Francisco to Chicago with 150 seats available. The number of requests for reservations usually exceeds the number of seats by a considerable amount. However, even though the fare is nonrefundable, an average of only 80 percent of the customers who make reservations actually show up to take the flight, so it seems appropriate to accept more reservations than can be flown. At the same time, significant costs are incurred if customers with reservations are not allowed to take the flight. Therefore, the company’s OR group is analyzing what number of reservations should be accepted to maximize the expected profit from the flight.

In the spreadsheet model in Fig. 28.16, the decision variable is Reservations To Accept (C13) and the results cell is Profit (F23). The OR group wants to consider integer values of the decision variable over the range between 150 and 200, so the parameter cell dialog box is used in the usual way to specify these bounds on the variable. The decision is made to test 11 values of Reservations To Accept (C13), so simulations will be run for values in intervals of five between 150 and 200.

The results are shown in Fig. 28.32. The parameter analysis report on the left side of the figure reveals that the mean of the profit values obtained in the respective simulation runs climbs rapidly as Reservations To Accept (C13) increases until the mean reaches a peak of $11,912 at 185 reservations, after which it starts to drop. Only the means at 180 and 190 reservations are close to this peak, so it seems clear that the most profitable num- ber of reservations lies somewhere between 180 and 190. (Now that the range of numbers that need to be considered has been narrowed down this far, Problem 28.10 asks you to continue that analysis by generating a parameter analysis report that considers all integer values over this range.)

The trend chart on the right side of Fig. 28.32 provides additional insight. The bands in this chart trend upward until the number of reservations to accept reaches approximately

INTRODUCTION TO OPERATIONS RESEARCH-0704

INTRODUCTION TO OPERATIONS RESEARCH-0705

185; then they start trending slowly downward. This indicates that the entire frequency distribution from the respective simulation runs keeps shifting upward until the run for 185 reservations and then starts shifting downward. Also note that the width of the entire set of seven bands increases until about the simulation run for 180 reservations and then remains about the same thereafter. This indicates that the amount of variability in the profit values also increases until the simulation run for 180 reservations and then remains about the same thereafter.

Comments

Post a Comment

Popular posts from this blog

DUALITY THEORY:THE ESSENCE OF DUALITY THEORY

By -
Image
THE ESSENCE OF DUALITY THEORY Given our standard form for the primal problem at the left (perhaps after conversion from another form), its dual problem has the form shown to the right. Thus, with the primal problem in maximizatio n form, the dual problem is in minimization form instead. Furthermore, the dual problem uses exactly the same pa r amete r s as the primal problem, but in different locations, as summarized below. 1. The coefficients in the objective function of the primal problem are the right-hand sides of the functional constraints in the dual problem. 2. The right-hand sides of the functional constraints in the primal problem are the coef- ficients in the objective function of the dual problem. 3. The coefficients of a variable in the functional constraints of the primal problem are the coefficients in a functional constraint of the dual problem. To highlight the comparison, now look at these same two problems in matrix notation (as introduced at the beginn...
Read more

NETWORK OPTIMIZATION MODELS:THE MINIMUM SPANNING TREE PROBLEM

By -
Image
THE MINIMUM SPANNING TREE PROBLEM The minimum spanning tree problem bears some similarities to the main version of the shortest-path problem presented in the preceding section. In both cases, an undi r ecte d and connected network is being considered, where the given information includes some mea- sure of the positive length (distance, cost, time, etc.) associated with each link. Both problems also involve choosing a set of links that have the shortest total length among all sets of links that satisfy a certain property. For the shortest-path problem, this property is that the chosen links must provide a path between the origin and the destination. For the minimum spanning tree problem, the required property is that the chosen links must provide a path between ea c h pair of nodes. The minimum spanning tree problem can be summarized as follows: 1. You are given the nodes of a network but not the links. Instead, you are given the po- tential links and the positive length for each ...
Read more

INTEGER PROGRAMMING:THE BRANCH-AND-CUT APPROACH TO SOLVING BIP PROBLEMS

By -
TH E BRANCH-AND-CUT APPROACH TO SOLVING BIP PROBLEMS Integer programming has been an especially exciting area of OR since the mid-1980s be- cause of the dramatic progress being made in its solution methodology. Background To place this progress into perspective, consider the historical background. One big break- through had come in the 1960s and early 1970s with the development and refinement of the branch-and-bound approach. But then the state of the art seemed to hit a plateau. Rel- atively small problems (well under 100 variables) could be solved very efficiently, but even a modest increase in problem size might cause an explosion in computation time be- yond feasible limits. Little progress was being made in overcoming this exponential growth in computation time as the problem size was increased. Many important problems arising in practice could not be solved. Then came the next breakthrough in the mid-1980s, with the introduction of the b r an c h- and-cu t approach to sol...
Read more