THE APPLICATION OF QUEUEING THEORY:FORMULATION OF WAITING-COST FUNCTIONS

FORMULATION OF WAITING-COST FUNCTIONS

To express E(WC) mathematically, we must first formulate a waiting-cost function that de- scribes how the actual waiting cost being incurred varies with the current behavior of the queue- ing system. The form of this function depends on the context of the individual problem. However, most situations can be represented by one of the two basic forms described next.

The g(N ) Form

Consider first the situation discussed in the preceding section where the queueing system customers are internal to the organization providing the service, and so the primary cost of waiting may be the lost profit from lost productivity. The rate at which productive output is lost sometimes is essentially proportional to the number of customers in the queueing sys- tem. However, in many cases there is not enough productive work available to keep all the members of the calling population continuously busy. Therefore, little productive output may be lost by having just a few members idle, waiting for service in the queueing system, whereas the loss may increase greatly if a few more members are made idle because they require service. Consequently, the primary property of the queueing system that determines the current rate at which waiting costs are being incurred is N, the number of customers in the system. Thus, the form of the waiting-cost function for this kind of situation is that il- lustrated in Fig. 26.5, namely, a function of N. We shall denote this form by g(N ).

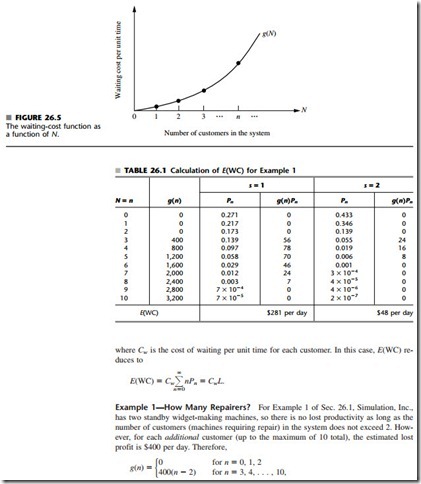
The g(N ) function is constructed for a particular situation by estimating g(n), the waiting-cost rate incurred when N = n, for n = 1, 2, . . . , where g(0) = 0. After com- puting the Pn probabilities for a given design of the queueing system, we can calculate

as shown in Table 26.1. Consequently, after calculating the Pn probabilities as described in Sec. 26.1, E(WC) is calculated by summing the rightmost column of Table 26.1 for each of the two cases of interest, namely, having one repairer (s = 1) or two repairers (s = 2).

The h('W) Form

Now consider the cases discussed in Sec. 26.2 where the queueing system customers are external to the organization providing the service. Three major types of queueing systems described in Sec. 17.3—commercial service systems, transportation service systems, and social service systems—typically fall into this category. In the case of commercial ser- vice systems, the primary cost of waiting may be the lost profit from lost future busi- ness. For transportation service systems and social systems, the primary cost of waiting may be in the form of a social cost. However, for either type of cost, its magnitude tends to be affected greatly by the size of the waiting times experienced by the customers. Thus, the primary property of the queueing system that determines the waiting cost cur- rently being incurred is 'W, the waiting time in the system for the individual customers. Consequently, the form of the waiting-cost function for this kind of situation is that il- lustrated in Fig. 26.6, namely, a function of 'W. We shall denote this form by h('W).

Note that the example of a h('W) function shown in Fig. 26.6 is a nonlinear function where the slope keeps increasing as 'W increases. Although h('W) sometimes is a simple linear function instead, it is fairly common to have this kind of nonlinear function. An in- creasing slope reflects a situation where the marginal cost of extending the waiting time keeps increasing. A customer may not mind a “normal” wait of reasonable length, in which case there may be virtually no negative consequences for the organization providing the service in terms of lost profit from lost future business, a social cost, etc. However, if the wait extends even further, the customer may become increasingly exasperated, perhaps even missing deadlines. In such a situation, the negative consequences to the organization may rapidly become relatively severe.

One way of constructing the h('W) function is to estimate h(w) (the waiting cost incurred when a customer’s waiting time 'W = w) for several values of w and then to fit a polynomial to these points. The expectation of this function of a continuous random vari- able is then defined as

E(h('W)) by the expected number of customers per unit time entering the queueing sys- tem. In particular, if the mean arrival rate is a constant A, then

Example 2—Which Computer? Because the faculty and students of Emerald Uni- versity would experience different turnaround times with the two computers under con- sideration (see Sec. 26.1), the choice between the computers required an evaluation of the consequences of making them wait for their jobs to be run. Therefore, several leading scientists on the faculty were asked to evaluate these consequences.

The scientists agreed that one major consequence is a delay in getting research done. Little effective progress can be made while one is awaiting the results from a computer run. The scientists estimated that it would be worth $500 to reduce this delay by a day. Therefore, this component of waiting cost was estimated to be $500 per day, that is, 500'W, where 'W is expressed in days.

The scientists also pointed out that a second major consequence of waiting is a break in the continuity of the research. Although a short delay (a fraction of a day) causes lit- tle problem in this regard, a longer delay causes significant wasted time in having to gear up to resume the research. The scientists estimated that this wasted time would be roughly proportional to the square of the delay time. Dollar figures of $100 and $400 were then imputed to the value of being able to avoid this consequence entirely rather than having a wait of 1 day and 1 day, respectively. Therefore, this component of the waiting cost was estimated to be 400'W2.

Note that this result is identical to the result when g(N ) is a linear function. Consequently, when the total waiting cost incurred by the queueing system is simply proportional to the total waiting time, it does not matter whether the g(N ) or the h( ) form is used for the waiting-cost function.

Example 3—How Many Tool Cribs? As indicated in Sec. 26.1, the value to the Mechanical Company of a busy mechanic’s output averages about $48 per hour. Thus, Cw 48. Consequently, for each tool crib the expected waiting cost per hour is

E(WC) 48L,

where L represents the expected number of mechanics waiting (or being served) at the tool crib.