Nonlinear Programming:NONCONVEX PROGRAMMING (WITH SPREADSHEETS)

NONCONVEX PROGRAMMING (WITH SPREADSHEETS)

The assumptions of convex programming (the function f(x) to be maximized is concave and all the gi(x) constraint functions are convex) are very convenient ones, because they ensure that any local maximum also is a global maximum. (If the objective is to minimize f(x) instead, then convex programming assumes that f(x) is convex, and so on, which en- sures that a local minimum also is a global minimum.) Unfortunately, the nonlinear pro- gramming problems that arise in practice frequently fail to satisfy these assumptions. What kind of approach can be used to deal with such nonconvex programming problems?

The Challenge of Solving Nonconvex Programming Problems

There is no single answer to the above question because there are so many different types of nonconvex programming problems. Some are much more difficult to solve than others. For example, a maximization problem where the objective function is nearly convex gener- ally is much more difficult than one where the objective function is nearly concave. (The SUMT example in Sec. 13.9 illustrated a case where the objective function was so close to being concave that the problem could be treated as if it were a convex programming problem.) Similarly, having a feasible region that is not a convex set (because some of the gi(x) functions are not convex) generally is a major complication. Dealing with functions that are not differentiable, or perhaps not even continuous, also tends to be a major complication.

The goal of much ongoing research is to develop efficient global optimization pro- cedures for finding a globally optimal solution for various types of nonconvex program- ming problems, and some progress has been made. As one example, LINDO Systems (which produces LINDO, LINGO, and What’sBest!) has incorporated a global optimizer into its advanced solver that is shared by some of its software products. In particular, LINGO and What’sBest! have a multistart option to automatically generate a number of starting points for their nonlinear programming solver in order to quickly find a good solution. If the global option is checked, they next employ the global optimizer. The global optimizer converts a nonconvex programming problem (including even those whose formulation in- cludes logic functions such as IF, AND, OR, and NOT) into several subproblems that are convex programming relaxations of portions of the original problem. The branch-and-bound technique then is used to exhaustively search over the subproblems. Once the procedure runs to completion, the solution found is guaranteed to be a globally optimal solution. (The other possible conclusion is that the problem has no feasible solutions.) The student ver- sion of this global optimizer is included in the version of LINGO that is provided on the book’s website. However, it is limited to relatively small problems (a maximum of five

An Application Vignette

Deutsche Post DHL is the largest logistics service provider worldwide. It employs over half a million peo- ple in more than 220 countries while delivering three mil- lion items and over 70 million letters each day with over 150,000 vehicles. The dramatic story of how DHL quickly achieved this lofty status is one that combines enlightened managerial leadership, an innovative marketing campaign, and the application of nonlinear programming to optimize the use of marketing resources.

Starting as just a German postal service, the com- pany’s senior management developed a visionary plan to begin the 21st century by transforming the company into a truly global logistics business. The first step was to acquire and integrate a number of similar companies that already had a strong presence in various other parts of the world. Because customers who operate on a global scale expect to deal with just one provider, the next step was to develop an aggressive marketing program based on extensive marketing research to rebrand DHL as a supe- rior truly global company that could fully meet the needs of these customers. These marketing activities were

pursued vigorously in more than 20 of the largest coun- tries on four continents.

This kind of marketing program is very expensive, so it is important to use the limited marketing resources as effectively as possible. Therefore, OR analysts devel- oped a brand choice model with an objective function that measures this effectiveness. Nonconvex program- ming then was implemented in a spreadsheet environ- ment to maximize this objective function without exceeding the total marketing budget.

This innovative use of marketing theory and nonlin- ear programming led to a substantial increase in the global brand value of DHL that enabled it to catapult into a market-leading position. This increase from 2003 to 2008 was estimated to be $1.32 billion (a 32 percent increase). The corresponding return on investment was 38 percent.

Source: M. Fischer, W. Giehl, and T. Freundt, “Managing Global Brand Investments at DHL,” Interfaces, 41(1): 35–50, Jan.–Feb. 2011. (A link to this article is provided on our web- site, www.mhhe.com/hillier.)

nonlinear variables out of 500 variables total). The professional version of the global op- timizer has successfully solved some much larger problems.

Similarly, MPL now supports a global optimizer called LGO. The student version of LGO is available to you as one of the MPL solvers provided on the book’s website. LGO also can be used to solve convex programming problems.

A variety of approaches to global optimization (such as the one incorporated into LINGO described above) are being tried. We will not attempt to survey this advanced topic in any depth. We instead will begin with a simple case and then introduce a more general approach at the end of the section. We will illustrate our methodology with spread- sheets and Excel software, but other software packages also can be used.

Using Solver to Find Local Optima

We now will focus on straightforward approaches to relatively simple types of non- convex programming problems. In particular, we will consider (maximization) problems where the objective function is nearly concave either over the entire feasible region or within major portions of the feasible region. We also will ignore the added complexity of having nonconvex constraint functions gi(x) by simply using linear constraints. We will begin by illustrating what can be accomplished by simply applying some algorithm for convex programming to such problems. Although any such algorithm (such as those described in Sec. 13.9) could be selected, we will use the convex programming algo- rithm that is employed by Solver for nonlinear programming problems.

For example, consider the following one-variable nonconvex programming problem:

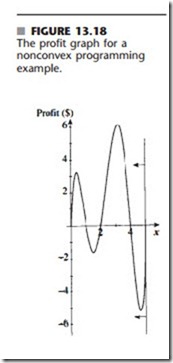
where Z represents the profit in dollars. Figure 13.18 shows a plot of the profit over the fea- sible region that demonstrates how highly nonconvex this function is. However, if this graph were not available, it might not be immediately clear that this is not a convex program- ming problem since a little analysis is required to verify that the objective function is not concave over the feasible region. Therefore, suppose that Solver’s GRG Nonlinear solving method, which is designed for solving convex programming problems, is applied to this example. (ASPE also has this same solving method and so would be applied in the same way.) Figure 13.19 demonstrates what a difficult time Solver has in attempting to cope with this problem. The model is straightforward to formulate in a spreadsheet, with x (C5) as the changing cell and Profit (C8) as the objective cell. (Note that GRG Nonlinear is chosen as the solving method.) When x = 0 is entered as the initial value in the chang- ing cell, the left spreadsheet in Fig. 13.19 shows that Solver then indicates that x = 0.371 is the optimal solution with Profit = $3.19. However, if x = 3 is entered as the initial value instead, as in the middle spreadsheet in Fig. 13.19, Solver obtains x = 3.126 as the optimal solution with Profit = $6.13. Trying still another initial value of x = 4.7 in the right spread- sheet, Solver now indicates an optimal solution of x = 5 with Profit = $0. What is going on here?

Figure 13.18 helps to explain Solver’s difficulties with this problem. Starting at x = 0, the profit graph does indeed climb to a peak at x = 0.371, as reported in the left spreadsheet of Fig. 13.19. Starting at x = 3 instead, the graph climbs to a peak at x = 3.126, which is the solution found in the middle spreadsheet. Using the right spreadsheet’s starting solution of x = 4.7, the graph climbs until it reaches the boundary imposed by the x < 5 constraint, so x = 5 is the peak in that direction. These three peaks are the local maxima (or local optima) because each one is a maximum of the graph within a local neighborhood of that point. How- ever, only the largest of these local maxima is the global maximum, that is, the highest point on the entire graph. Thus, the middle spreadsheet in Fig. 13.19 did succeed in finding the globally optimal solution at x = 3.126 with Profit = $6.13.

Solver uses the generalized reduced gradient method, which adapts the gradient search method described in Sec. 13.5 to solve convex programming problems. Therefore, this algo- rithm can be thought of as a hill-climbing procedure. It starts at the initial solution entered into the changing cells and then begins climbing that hill until it reaches the peak (or is blocked

from climbing further by reaching the boundary imposed by the constraints). The procedure terminates when it reaches this peak (or boundary) and reports this solution. It has no way of detecting whether there is a taller hill somewhere else on the profit graph.

The same thing would happen with any other hill-climbing procedure, such as SUMT (described in Sec. 13.9), that stops when it finds a local maximum. Thus, if SUMT were to be applied to this example with each of the three initial trial solutions used in Fig. 13.19, it would find the same three local maxima found by Solver.

A More Systematic Approach to Finding Local Optima

A common approach to “easy” nonconvex programming problems is to apply some algorith- mic hill-climbing procedure that will stop when it finds a local maximum and then to restart it a number of times from a variety of initial trial solutions (either chosen randomly or as a systematic cross-section) in order to find as many distinct local maxima as possible. The best of these local maxima is then chosen for implementation. Normally, the hill-climbing proce- dure is one that has been designed to find a global maximum when all the assumptions of con- vex programming hold, but it also can operate to find a local maximum when they do not.

Solver includes an automated way of trying multiple starting points. In Excel’s Solver, clicking on the Options button in Solver and then choosing the GRG Nonlinear tab brings up the Options dialog box shown in Fig. 13.20. Selecting the Use Multistart option causes Solver to randomly select 100 different starting points. (The number of starting points can be varied by changing the Population Size option.) In ASPE’s Solver, these options are available on the Engine tab in the Model pane. When Multistart is enabled, Solver then provides the best solution found after solving with each of the different starting points.

Unfortunately, there generally is no guarantee of finding a globally optimal solution, no matter how many different starting points are tried. Also, if the profit graphs are not smooth (e.g., if they have discontinuities or kinks), then Solver may not even be able to find local optima when using GRG Nonlinear as the solving method. Fortunately, both ASPE and re- cent versions of Excel's Solver provide another search procedure, called Evolutionary Solver, to attempt to solve these somewhat more difficult nonconvex programming problems.

Evolutionary Solver

Both ASPE’s Solver and the standard Excel Solver (for Excel 2010 and newer) include a search procedure called Evolutionary Solver in the set of tools available to search for an optimal solution for a model. The philosophy of Evolutionary Solver is based on genetics, evolution, and the survival of the fittest. Hence, this type of algorithm is sometimes called a genetic algorithm. We will devote Sec. 14.4 to describing how genetic algorithms operate.

Evolutionary Solver has three crucial advantages over the standard Solver (or any other convex programming algorithm) for solving nonconvex programming problems. First, the complexity of the objective function does not impact Evolutionary Solver. As long as the function can be evaluated for a given trial solution, it does not matter if the function has kinks or discontinuities or many local optima. Second, the complexity of the given con- straints (including even nonconvex constraints) also doesn’t substantially impact Evolu- tionary Solver (although the number of constraints does). Third, because it evaluates whole populations of trial solutions that aren’t necessarily in the same neighborhood as the cur- rent best trial solution, Evolutionary Solver keeps from getting trapped at a local optimum. In fact, Evolutionary Solver is guaranteed to eventually find a globally optimal solution for any nonlinear programming problem (including nonconvex programming problems), if it is run forever (which is impractical of course). Therefore, Evolutionary Solver is well suited for dealing with many relatively small nonconvex programming problems.

On the other hand, it must be pointed out that Evolutionary Solver is not a panacea. First, it can take much longer than the standard Solver to find a final solution. Second, Evolutionary Solver does not perform well on models that have many constraints. Third, Evolutionary Solver is a random process, so running it again on the same model usually will yield a different final solution. Finally, the best solution found typically is not quite optimal (although it may be very close). Evolutionary Solver does not continuously move toward better solutions. Rather it is more like an intelligent search engine, trying out dif- ferent random solutions. Thus, while it is quite likely to end up with a solution that is very close to optimal, it almost never returns the exact globally optimal solution on most types of nonlinear programming problems. Consequently, if often can be beneficial to run Solver with the GRG Nonlinear option after the Evolutionary Solver, starting with the fi- nal solution obtained by the Evolutionary Solver, to see if this solution can be improved by searching around its neighborhood.