MARKOV CHAINS:CONTINUOUS TIME MARKOV CHAINS

By -

CONTINUOUS TIME MARKOV CHAINS

In all the previous sections, we assumed that the time parameter t was discrete (that is, t = 0, 1, 2, . . .). Such an assumption is suitable for many problems, but there are certain cases (such as for some queueing models considered in Chap. 17) where a continuous time parameter (call it t') is required, because the evolution of the process is being observed continuously over time. The definition of a Markov chain given in Sec. 29.2 also extends to such continuous processes. This section focuses on describing these “continuous time Markov chains” and their properties.

INTRODUCTION TO OPERATIONS RESEARCH-0738

INTRODUCTION TO OPERATIONS RESEARCH-0739

INTRODUCTION TO OPERATIONS RESEARCH-0740

Steady-State Probabilities

Just as the transition probabilities for a discrete time Markov chain satisfy the Chapman- Kolmogorov equations, the continuous time transition probability function also satisfies these equations. Therefore, for any states i and j and nonnegative numbers t and s (0 < s < t),

INTRODUCTION TO OPERATIONS RESEARCH-0741

The steady-state equation for state j has an intuitive interpretation. The left-hand side (wj qj) is the rate at which the process leaves state j, since wj is the (steady-state) proba- bility that the process is in state j and qj is the transition rate out of state j given that the process is in state j. Similarly, each term on the right-hand side (wi qij) is the rate at which the process enters state j from state i, since qij is the transition rate from state i to state j given that the process is in state i. By summing over all i -:: j, the entire right-hand side then gives the rate at which the process enters state j from any other state. The overall equation thereby states that the rate at which the process leaves state j must equal the rate at which the process enters state j. Thus, this equation is analogous to the conservation of flow equations encountered in many engineering and science courses.

Because each of the first M + 1 steady-state equations requires that two rates be in balance (equal), these equations sometimes are called the balance equations.

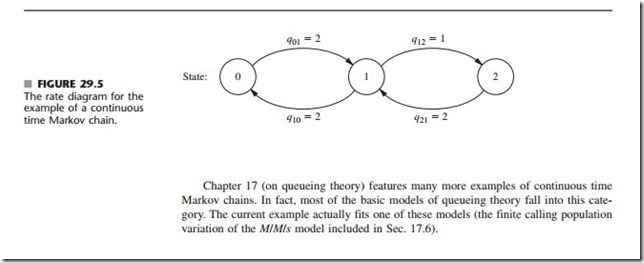
Example. A certain shop has two identical machines that are operated continuously except when they are broken down. Because they break down fairly frequently, the top- priority assignment for a full-time maintenance person is to repair them whenever needed.

The time required to repair a machine has an exponential distribution with a mean of -- day. Once the repair of a machine is completed, the time until the next breakdown of that machine has an exponential distribution with a mean of 1 day. These distributions are independent.

Define the random variable X(t') as X(t') = number of machines broken down at time t', so the possible values of X(t') are 0, 1, 2. Therefore, by letting the time parameter t' run continuously from time 0, the continuous time stochastic process {X(t'); t'> 0} gives the evolution of the number of machines broken down.

Because both the repair time and the time until a breakdown have exponential distributions, {X(t'); t'> 0} is a continuous time Markov chain5 with states 0, 1, 2. Consequently, we can use the steady-state equations given in the preceding subsection to find the steady-state probability distribution of the number of machines broken down. To do this, we need to determine all the transition rates, i.e., the qi and qij for i, j = 0, 1, 2.

The state (number of machines broken down) increases by 1 when a breakdown occurs and decreases by 1 when a repair occurs. Since both breakdowns and repairs occur one at a time, q = 0 and q = 0. The expected repair time is 1 day, so the rate at which repairs are completed (when any machines are broken down) is 2 per day, which implies that q21 = 2 and q10 = 2. Similarly, the expected time until a particular operational machine breaks down is 1 day, so the rate at which it breaks down (when operational) is 1 per day, which implies that q12 = 1. During times when both machines are operational, breakdowns occur at the rate of 1 + 1 = 2 per day, so q01 = 2.

These transition rates are summarized in the rate diagram shown in Fig. 29.5. These rates now can be used to calculate the total transition rate out of each state.

INTRODUCTION TO OPERATIONS RESEARCH-0742

Thus, in the long run, both machines will be broken down simultaneously 20 percent of the time, and one machine will be broken down another 40 percent of the time.

5Proving this fact requires the use of two properties of the exponential distribution discussed in Sec. 17.4 (lack of memory and the minimum of exponentials is exponential), since these properties imply that the Tij random variables introduced earlier do indeed have exponential distributions.

INTRODUCTION TO OPERATIONS RESEARCH-0743

Comments

Post a Comment

Popular posts from this blog

DUALITY THEORY:THE ESSENCE OF DUALITY THEORY

By -
Image
THE ESSENCE OF DUALITY THEORY Given our standard form for the primal problem at the left (perhaps after conversion from another form), its dual problem has the form shown to the right. Thus, with the primal problem in maximizatio n form, the dual problem is in minimization form instead. Furthermore, the dual problem uses exactly the same pa r amete r s as the primal problem, but in different locations, as summarized below. 1. The coefficients in the objective function of the primal problem are the right-hand sides of the functional constraints in the dual problem. 2. The right-hand sides of the functional constraints in the primal problem are the coef- ficients in the objective function of the dual problem. 3. The coefficients of a variable in the functional constraints of the primal problem are the coefficients in a functional constraint of the dual problem. To highlight the comparison, now look at these same two problems in matrix notation (as introduced at the beginn...
Read more

NETWORK OPTIMIZATION MODELS:THE MINIMUM SPANNING TREE PROBLEM

By -
Image
THE MINIMUM SPANNING TREE PROBLEM The minimum spanning tree problem bears some similarities to the main version of the shortest-path problem presented in the preceding section. In both cases, an undi r ecte d and connected network is being considered, where the given information includes some mea- sure of the positive length (distance, cost, time, etc.) associated with each link. Both problems also involve choosing a set of links that have the shortest total length among all sets of links that satisfy a certain property. For the shortest-path problem, this property is that the chosen links must provide a path between the origin and the destination. For the minimum spanning tree problem, the required property is that the chosen links must provide a path between ea c h pair of nodes. The minimum spanning tree problem can be summarized as follows: 1. You are given the nodes of a network but not the links. Instead, you are given the po- tential links and the positive length for each ...
Read more

INTEGER PROGRAMMING:THE BRANCH-AND-CUT APPROACH TO SOLVING BIP PROBLEMS

By -
TH E BRANCH-AND-CUT APPROACH TO SOLVING BIP PROBLEMS Integer programming has been an especially exciting area of OR since the mid-1980s be- cause of the dramatic progress being made in its solution methodology. Background To place this progress into perspective, consider the historical background. One big break- through had come in the 1960s and early 1970s with the development and refinement of the branch-and-bound approach. But then the state of the art seemed to hit a plateau. Rel- atively small problems (well under 100 variables) could be solved very efficiently, but even a modest increase in problem size might cause an explosion in computation time be- yond feasible limits. Little progress was being made in overcoming this exponential growth in computation time as the problem size was increased. Many important problems arising in practice could not be solved. Then came the next breakthrough in the mid-1980s, with the introduction of the b r an c h- and-cu t approach to sol...
Read more