EXAMPLES OF PERFORMING SIMULATIONS ON SPREADSHEETS WITH ANALYTIC SOLVER PLATFORM:FINANCIAL RISK ANALYSIS

By -

FINANCIAL RISK ANALYSIS

One of the earliest areas of application of simulation, dating back to the 1960s, was financial risk analysis. This continues today to be one of the most important areas of application.

When assessing any financial investment (or a portfolio of investments), the key trade- off is between the return from the investment and the risk associated with the investment. Of these two quantities, the less difficult one to determine is the return that would be obtained if everything evolves as currently projected. However, assessing the risk is relatively difficult. Fortunately, simulation is ideally suited to perform this risk analysis by obtaining a risk profile, namely, a frequency distribution of the return from the investment. The portion of the frequency distribution that reflects an unfavorable return clearly describes the risk associated with the investment.

The following example illustrates this approach in the context of real estate investments. Like the Everglade example in the preceding section, you will see simulation being used to refine prior analysis done by linear programming because this prior analysis was unable to take the uncertainty in future cash flows into account.

The Think-Big Financial Risk Analysis Problem

The Think-Big Development Co. is a major investor in commercial real estate development projects. It has been considering taking a share in three large construction projects— a high-rise office building, a hotel, and a shopping center. In each case, the partners in the project would spend three years with the construction, then retain ownership for three years while establishing the property, and then sell the property in the seventh year. By using estimates of expected cash flows, as well as constraints on the amounts of investment capital available both now and over the next three years, linear programming has been applied to obtain the following proposal for how big a share Think-Big should take in each of these projects:

Proposal

Do not take any share of the high-rise building project. Take a 16.50 percent share of the hotel project.

Take a 13.11 percent share of the shopping center project.

This proposal is estimated to return a net present value (NPV) of $18.11 million to Think- Big.

However, Think-Big management understands very well that such decisions should not be made without taking risk into account. These are very risky projects since it is unclear how well these properties will compete in the marketplace when they go into operation in a few years. Although the construction costs during the first three years can be estimated fairly roughly, the net incomes during the following three years of operation are very uncertain. Consequently, there is an extremely wide range of possible values for each sale price in year 7. Therefore, management wants risk analysis to be performed in the usual way (with simulation) to obtain a risk profile of what the total NPV might actually turn out to be with this proposal.

To perform this risk analysis, Think-Big staff now has devoted considerable time to estimating the amount of uncertainty in the cash flows for each project over the next seven years. These data are summarized in Table 28.2 (in units of millions of dollars) for a 100 percent share of each project. Thus, when taking a smaller percentage share of a project, the numbers in the table should be reduced proportionally to obtain the relevant numbers

for Think-Big. In years 1 through 6 for each project, the probability distribution of cash flow is assumed to be a normal distribution, where the first number shown is the estimated mean and the second number is the estimated standard deviation of the distribution. In year 7, the income from the sale of the property is assumed to have a uniform distribution over the range from the first number shown to the second number shown.

To compute NPV, a cost of capital of 10 percent per annum is being used. Thus, the cash flow in year n is divided by (1.1)n before adding these discounted cash flows to obtain NPV.

A Spreadsheet Model for Applying Simulation

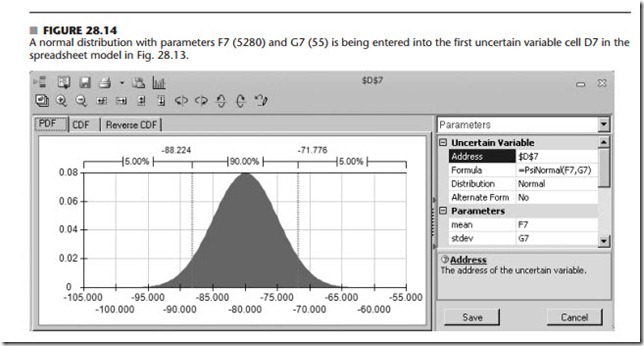
A spreadsheet model has been formulated for this problem in Fig. 28.13. There is no uncertainty about the immediate (year 0) cash flows appearing in cells D6 and D16, so these are data cells. However, because of the uncertainty for years 1–7, cells D7:D13 and D17:D23 containing the simulated cash flows for these years need to be uncertain variable cells. (The numbers in these cells in Fig. 28.13 represent one possible random outcome— the last trial of the simulation run.) Table 28.2 specifies the probability distributions and their parameters that have been estimated for these cash flows, so the form of the distributions has been recorded in cells E7:E13 and E17:E23 while entering the corresponding parameters in cells F7:G13 and F17:G23. Figure 28.14 shows the Normal Distribution dialog box that is used to enter the parameters (mean and standard deviation) for the normal distribution into the first uncertain variable cell D7 by referencing cells F7 and G7. The formula in D7 is then copied and pasted into cells D8:D12 and D17:D22 to define these uncertain variable cells. The Uniform Distribution dialog box (like the similar one dis- played earlier in Fig. 20.9 for an integer uniform distribution) is used in a similar way to enter the parameters (minimum and maximum) for this kind of distribution into the uncer- tain variable cells D13 and D23.

The simulated cash flows in cells D6:D13 and D16:D23 are for 100 percent of the hotel project and the shopping center project, respectively, so Think-Big’s share of these cash flows needs to be reduced proportionally based on its shares in these projects. The proposal being analyzed is to take the shares shown in cells H28:H29. The equations entered into cells D28:D35 (see the bottom of Fig. 28.13) then gives Think-Big’s total cash flow in the respective years for its share of the two projects.

Think-Big’s management wants to obtain a risk profile of what the total net present value (NPV) might be with this proposal. Therefore, the results cell is NetPresent Value (D37). To show the mean NPV over the simulation run, MeanNPV (D39) is defined as a statistic cell.

INTRODUCTION TO OPERATIONS RESEARCH-0683

INTRODUCTION TO OPERATIONS RESEARCH-0684INTRODUCTION TO OPERATIONS RESEARCH-0685

The Simulation Results

Using the Simulation Options dialog box to specify 1,000 trials, Fig. 28.15 shows the results of applying simulation to the spreadsheet model in Fig. 28.13. The frequency chart in Fig. 28.15 provides the risk profile for the proposal since it shows the relative likelihood of the various values of NPV, including those where NPV is negative. The mean is $18.120 million, which is very attractive. However, the 1,000 trials generated an extremely wide range of NPV values, all the way from about –$28 million to over $62 million. Thus, there is a significant chance of incurring a huge loss. By entering 0 into the box in the Upper Cutoff box of the statistics table, the Likelihood box indicates that 81 percent of the trials resulted in a profit (a positive value of NPV). This also gives the bad news that there is roughly a 19 percent chance of incurring a loss of some size. The lightly shaded portion of the chart to the left of 0 shows that most of the trials with losses involved losses up to about $10 million, but that quite a few trials had losses that ranged from $10 million to nearly $30 million.

Armed with all this information, a managerial decision now can be made about whether the likelihood of a sizable profit justifies the significant risk of incurring a loss and perhaps even a very substantial loss. Thus, the role of simulation is to provide the information needed for making a sound decision, but it is management that uses its best judgment to make the decision.

INTRODUCTION TO OPERATIONS RESEARCH-0686

 

INTRODUCTION TO OPERATIONS RESEARCH-0687

Comments

Post a Comment

Popular posts from this blog

DUALITY THEORY:THE ESSENCE OF DUALITY THEORY

By -
Image
THE ESSENCE OF DUALITY THEORY Given our standard form for the primal problem at the left (perhaps after conversion from another form), its dual problem has the form shown to the right. Thus, with the primal problem in maximizatio n form, the dual problem is in minimization form instead. Furthermore, the dual problem uses exactly the same pa r amete r s as the primal problem, but in different locations, as summarized below. 1. The coefficients in the objective function of the primal problem are the right-hand sides of the functional constraints in the dual problem. 2. The right-hand sides of the functional constraints in the primal problem are the coef- ficients in the objective function of the dual problem. 3. The coefficients of a variable in the functional constraints of the primal problem are the coefficients in a functional constraint of the dual problem. To highlight the comparison, now look at these same two problems in matrix notation (as introduced at the beginn...
Read more

NETWORK OPTIMIZATION MODELS:THE MINIMUM SPANNING TREE PROBLEM

By -
Image
THE MINIMUM SPANNING TREE PROBLEM The minimum spanning tree problem bears some similarities to the main version of the shortest-path problem presented in the preceding section. In both cases, an undi r ecte d and connected network is being considered, where the given information includes some mea- sure of the positive length (distance, cost, time, etc.) associated with each link. Both problems also involve choosing a set of links that have the shortest total length among all sets of links that satisfy a certain property. For the shortest-path problem, this property is that the chosen links must provide a path between the origin and the destination. For the minimum spanning tree problem, the required property is that the chosen links must provide a path between ea c h pair of nodes. The minimum spanning tree problem can be summarized as follows: 1. You are given the nodes of a network but not the links. Instead, you are given the po- tential links and the positive length for each ...
Read more

INTEGER PROGRAMMING:THE BRANCH-AND-CUT APPROACH TO SOLVING BIP PROBLEMS

By -
TH E BRANCH-AND-CUT APPROACH TO SOLVING BIP PROBLEMS Integer programming has been an especially exciting area of OR since the mid-1980s be- cause of the dramatic progress being made in its solution methodology. Background To place this progress into perspective, consider the historical background. One big break- through had come in the 1960s and early 1970s with the development and refinement of the branch-and-bound approach. But then the state of the art seemed to hit a plateau. Rel- atively small problems (well under 100 variables) could be solved very efficiently, but even a modest increase in problem size might cause an explosion in computation time be- yond feasible limits. Little progress was being made in overcoming this exponential growth in computation time as the problem size was increased. Many important problems arising in practice could not be solved. Then came the next breakthrough in the mid-1980s, with the introduction of the b r an c h- and-cu t approach to sol...
Read more