MARKOV CHAINS:CHAPMAN-KOLMOGOROV EQUATIONS

By -

CHAPMAN-KOLMOGOROV EQUATIONS

Section 29.2 introduced the n-step transition probability p(n). The following Chapman- Kolmogorov equations provide a method for computing these n-step transition probabilities:

INTRODUCTION TO OPERATIONS RESEARCH-0715

3These equations also hold in a trivial sense when m = 0 or m = n, but m = 1, 2, . . . , n - 1 are the only interesting cases.

These equations point out that in going from state i to state j in n steps, the process

INTRODUCTION TO OPERATIONS RESEARCH-0716

Thus, if the weather is in state 0 (dry) on a particular day, the probability of being in state 0 two days later is 0.76 and the probability of being in state 1 (rain) then is 0.24. Similarly, if the weather is in state 1 now, the probability of being in state 0 two days later is 0.72 whereas the probability of being in state 1 then is 0.28.

The probabilities of the state of the weather three, four, or five days into the future also can be read in the same way from the three-step, four-step, and five-step transition matrices calculated to three significant digits below.

INTRODUCTION TO OPERATIONS RESEARCH-0717

Note that the five-step transition matrix has the interesting feature that the two rows have identical entries (after rounding to three significant digits). This reflects the fact that the probability of the weather being in a particular state is essentially independent of the state of the weather five days before. Thus, the probabilities in either row of this five-step transition matrix are referred to as the steady-state probabilities of this Markov chain.

We will expand further on the subject of the steady-state probabilities of a Markov chain, including how to derive them more directly, at the beginning of Sec. 29.5.

INTRODUCTION TO OPERATIONS RESEARCH-0718

For example, given that there is one camera left in stock at the end of a week, the probability is 0.282 that there will be no cameras in stock 4 weeks later, that is, p(4) = 0.282. Similarly, given that there are two cameras left in stock at the end of a week, the probability is 0.171 that there will be three cameras in stock 4 weeks later, that is, p(4) = 0.171.

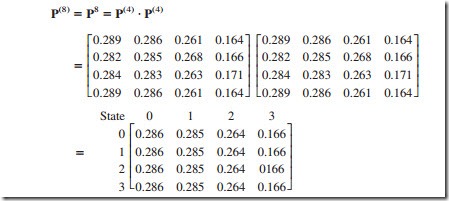
The transition probabilities for the number of cameras in stock 8 weeks from now can be read in the same way from the eight-step transition matrix calculated below.

INTRODUCTION TO OPERATIONS RESEARCH-0719

Like the five-step transition matrix for the weather example, this matrix has the interesting feature that its rows have identical entries (after rounding). The reason once again is that probabilities in any row are the steady-state probabilities for this Markov chain, i.e., the probabilities of the state of the system after enough time has elapsed that the initial state is no longer relevant.

Your IOR Tutorial includes a procedure for calculating P(n) = Pn for any positive integer n :s 99.

Unconditional State Probabilities

Recall that one- or n-step transition probabilities are conditional probabilities; for example, P{Xn = j⏐X0 = i} = p(n). Assume that n is small enough that these conditional probabilities are not yet steady-state probabilities. In this case, if the unconditional probability P{Xn = j} is desired, it is necessary to specify the probability distribution of the initial state, namely, P{X0 = i} for i = 0, 1, . . . , M. Then
INTRODUCTION TO OPERATIONS RESEARCH-0720
 

 

 

 

 

 

 

 

Comments

Post a Comment

Popular posts from this blog

DUALITY THEORY:THE ESSENCE OF DUALITY THEORY

By -
Image
THE ESSENCE OF DUALITY THEORY Given our standard form for the primal problem at the left (perhaps after conversion from another form), its dual problem has the form shown to the right. Thus, with the primal problem in maximizatio n form, the dual problem is in minimization form instead. Furthermore, the dual problem uses exactly the same pa r amete r s as the primal problem, but in different locations, as summarized below. 1. The coefficients in the objective function of the primal problem are the right-hand sides of the functional constraints in the dual problem. 2. The right-hand sides of the functional constraints in the primal problem are the coef- ficients in the objective function of the dual problem. 3. The coefficients of a variable in the functional constraints of the primal problem are the coefficients in a functional constraint of the dual problem. To highlight the comparison, now look at these same two problems in matrix notation (as introduced at the beginn...
Read more

NETWORK OPTIMIZATION MODELS:THE MINIMUM SPANNING TREE PROBLEM

By -
Image
THE MINIMUM SPANNING TREE PROBLEM The minimum spanning tree problem bears some similarities to the main version of the shortest-path problem presented in the preceding section. In both cases, an undi r ecte d and connected network is being considered, where the given information includes some mea- sure of the positive length (distance, cost, time, etc.) associated with each link. Both problems also involve choosing a set of links that have the shortest total length among all sets of links that satisfy a certain property. For the shortest-path problem, this property is that the chosen links must provide a path between the origin and the destination. For the minimum spanning tree problem, the required property is that the chosen links must provide a path between ea c h pair of nodes. The minimum spanning tree problem can be summarized as follows: 1. You are given the nodes of a network but not the links. Instead, you are given the po- tential links and the positive length for each ...
Read more

INTEGER PROGRAMMING:THE BRANCH-AND-CUT APPROACH TO SOLVING BIP PROBLEMS

By -
TH E BRANCH-AND-CUT APPROACH TO SOLVING BIP PROBLEMS Integer programming has been an especially exciting area of OR since the mid-1980s be- cause of the dramatic progress being made in its solution methodology. Background To place this progress into perspective, consider the historical background. One big break- through had come in the 1960s and early 1970s with the development and refinement of the branch-and-bound approach. But then the state of the art seemed to hit a plateau. Rel- atively small problems (well under 100 variables) could be solved very efficiently, but even a modest increase in problem size might cause an explosion in computation time be- yond feasible limits. Little progress was being made in overcoming this exponential growth in computation time as the problem size was increased. Many important problems arising in practice could not be solved. Then came the next breakthrough in the mid-1980s, with the introduction of the b r an c h- and-cu t approach to sol...
Read more