METHODS ENGINEERING:Between-Operations Analysis

Between-Operations Analysis

This section will discuss flow diagrams, multiactivity charts, arrangement (layout) of equipment, and balancing flow lines.

3.4.1. Flow Diagrams

Flow diagrams and their associated process charts are a technique for visually organizing and struc- turing an overview (‘‘mountaintop’’ view) of a between-workstations problem. There are three types: single object, assembly / disassembly, and action–decision.

3.4.1.1. Single Object Figure 8 shows a single-object process chart following a housing in a machine shop; the single object also can be a person. Some examples of following a person are vacuuming an office and unloading a semitrailer.

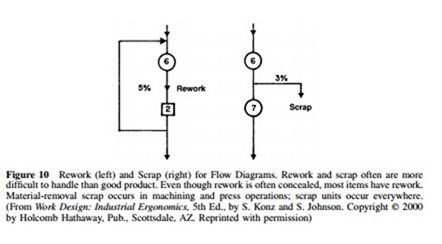
Figure 9 shows the five standard symbols for process charts. Some people put a number inside each symbol (identifying operation 1, 2, 3) and some don’t. Some people emphasize ‘‘do’’ operations by darkening those circles (but not get-ready and put-away operations) and some don’t. Since a process chart is primarily a communication tool for yourself, take your choice. Most operations have scrap and rework; Figure 10 shows how to chart them. At the end of the chart, summarize the number of operations, moves (including total distance), inspections, storages and delays. Estimate times for storages (which are planned) and delays (which are unplanned storages). Since this is a big-picture analysis, detailed times for operations and inspections normally are not recorded.

Next you would consider possible improvements using Kipling’s six honest men (who, what, where, why, when and how), SEARCH, and various checklists. This may lead to a proposed method where you would show reductions in number of operations, inspections, storages, distance moved, and so on. Because flow diagrams organize complex information and thus are a useful communication tool, you may want to make a polished copy of the flow diagrams to show to others. Since many potential improvements involve reducing movements between workstations, a map showing the move- ments is useful; Figure 11 shows a flow diagram of Joe College making a complex job of drinking beer in his apartment. Generally a sketch on cross-section paper is sufficient.

3.4.1.2. Assembly / Disassembly Diagrams Assembly flow diagrams (see Figure 12) tend to point out the problems of disorganized storage and movements. Figure 13 shows a disassembly diagram; another example would be in packing houses.

3.4.1.3. Action–Decision Diagrams In some cases, you may wish to study decision making; then consider an action–decision diagram (see Figure 14) or a decision structure table (see Section 3.5.2).

3.4.2. Multiactivity Charts

The purpose of a multiactivity chart is to improve utilization of multiple related activities. See Figure

15. The two or more activities (column headings) can be people or machines; they can also be parts of a person (left hand vs. right hand) or parts of a machine (cutting head vs. fixture 1 vs. fixture 2).

The time axis (drawn to a convenient scale) can be seconds, minutes, or hours.

Example charts and columns might be milling a casting (operator, machine), cashing checks (cashier, customer 1, customer 2), and serving meals (customer, server, cook).

For each column, give cycles / year, cost / minute, and percent idle. Make the idle time distinctive by cross-hatching, shading, or coloring red.

Improve utilization by (1) reducing idle time in a column, (2) shifting idle time from one column to another, or (3) decreasing idle time of an expensive component (such as person) by increasing idle time of a machine. McDonald’s uses this third concept when they have two dispensers of Coke

in order to reduce the waiting time of the order taker (and thus the customer).

Some time is considered to be free. For example, ‘‘inside machine time’’ describes the situation in which an operator is given tasks while the machine is operating. Since the operator is at the machine anyway, these tasks are ‘‘free.’’ A McDonald’s example is to grasp a lid while the cup is filling.

As pointed out above in (3), it is possible to have more than one machine / operator—this is double tooling. For example, use two sets of load / unload fixtures on an indexing fixture to reduce idle time while waiting for the machine to cut. Or one person can service two machines (i.e., 1 operator / 2 machines or 0.5 operator / machine). It is also possible to have 0.67 or 0.75 operators / machine. Do this by assigning 2 people / 3 machines or 3 / 4, that is, having the workers work as a team, not as individuals. This will require cross-trained operators, which is very useful when someone is absent.

Kitting is the general strategy of gathering components before assembly to minimize search-and- select operations and ensure that there are no missing parts. Subassemblies also may be useful. McDonald’s Big Mac has a ‘‘special sauce,’’ which is just a mixture of relish and mayonnaise, premixed to ensure consistency.

A disadvantage of the multiactivity chart is that it requires a standardized situation. Nonstandar- dized situations are difficult to show. For them, use computer simulation.

3.4.3. Arrangement (Layout) of Equipment

This section describes location of one item in an existing network. Arrangement of the entire facility is covered in Chapter 55.

Problem. Table 15 shows some examples of locating one item in an existing network of custom- ers. The item can be a person, a machine, or even a building. The network of customers can be people, machines, or buildings. The criterion minimized is usually distance moved but could be energy lost or time to reach a customer.

Typically an engineer is interested in finding the location that minimizes the distance moved—a minisum problem. An example would be locating a copy machine in an office. An alternative objec-

tive is to minimize the maximum distance—a minimax or worst-case problem. An example minimax problem would be to locate an ambulance so everyone could be reached in no more than 15 minutes. There is extensive analytical literature on this ‘‘planar single-facility location problem’’; see Francis et al. (1992, chap. 4).

The following is not elegant math but ‘‘brute force’’ calculations. The reason is that, using a hand calculator, the engineer can solve all reasonable alternatives in a short time—say 20 minutes. Then, using the calculated optimum for the criterion of distance, the designer should consider other criteria (such as capital cost, maintenance cost) before making a recommended solution.

Solution. The following example considers (1) the item to be located as a machine tool, (2) the network of customers (circles in Figure 16) as other machine tools with which the new tool will exchange product, and (3) the criterion to be minimized as distance moved by the product.

In most real problems, there are only a few possible places to put the new item; the remaining space is already filled with machines, building columns, aisles, and so forth. Assume there are only two feasible locations for the new item—the A and B rectangles in Figure 16.

Travel between a customer and A or B can be (1) straight line (e.g., conveyors), (2) rectangular (e.g., fork trucks using aisles), or (3) measured on a map (e.g., fork trucks using one-way aisles, conveyors following nondirect paths). Travel may be a mixture of the three types.

Some customers are more important than others, and thus the distance must be weighted. For a factory, an index could be pallets moved per month. For location of a fire station, the weight of a customer might depend on number of people occupying the site or the fire risk.

The movement cost of locating the new item at a specific feasible location is:

Ck = cost / unit distance (excluding Lk)

Assume, for customers 1, 2, and 3, that Lk = $0.50 / trip and Ck = $0.001 / m; for customers 4, 5, and 6, Lk = $1 / trip and Ck = $0.002 / m. Then the cost for alternative A = $854 + $79.07 =

$933.07 while the cost for B = $854 + $117.89 = $971.89. Thus, B has a movement cost of 104% of A. When making the decision where to locate the new item, use not only the movement cost but also installation cost, capital cost, and maintenance cost. Note that the product (WGTH)(DIST) (that is, the $854) is independent of the locations; it just adds a constant value to each alternative.

Cost need not be expressed in terms of money. Consider locating a fire station where the customers are parts of the town and the weights are expected number of trips in a l0-year period. Then load might be 1 min to respond to a call, travel 1.5 min / km, and unload 1 min; the criterion is to minimize mean time / call.

The distance cost might rise by a power of 2 (the inverse square law) for problems such as location of a siren or light.

3.4.4. Balancing Flow Lines

The two most common arrangements of equipment are a job shop and a flow line (often an assembly line). The purpose of balancing a flow line is to minimize the total idle time (balance delay time). There are three givens: (1) a table of work elements with their associated times (see Table 18), (2) a precedence diagram showing the element precedence relationships (see Figure 18), and (3) required

Each element time is assumed constant. In practice, each element time is a distribution.

units / minute from the line. The three unknowns are (1) the number of stations, (2) the number of workers at each station, and (3) the elements to be done at each station.

1. What is the total number to be made, and in how long a time? For example, 20,000 units could be made in 1000 hr at the rate of 20 / hr, 500 hr at 40 / hr, or some other combination. Continuous production is only one of many alternatives; a periodic shutdown might be best. Assume we wish to make 20,000 units in 1000 hr at the rate of 20 / hr. Then each station will take 1000 hr / 20,000 units = 0.05 hr / unit; cycle time is .05 hr.

2. Guess an approximate number of workstations by dividing total work time by cycle time: 0.1818 hr / 0.05 hr / station = 3.63 stations. Then use 4 workstations with 1 operator at each.

3. Make a trial solution as in Table 19 and Figure 19. Remembering not to violate precedence, identify each station with a cross-hatched area. Then calculate the idle percentage: 0.0182 / (4 X 0.05) = 9.1%.

But this can be improved. Consider Table 20. Here stations 1 and 2 are combined into one superstation with two operators. Elemental time now totals 0.0950. Since there are two operators, the

From Work Design: Industrial Ergonomics, 5th Ed., by S. Konz and S. Johnson. Copyright © 2000 by Holcomb Hathaway, Pub., Scottsdale, AZ. Reprinted with permission.

Cycle time = 0.0500 hr.

idle time / operator is 0.0025. So far there is no improvement over the solution of Table 19. But there is idle time at each station. Thus, the line cycle time can be reduced to 0.0475. The new idle time becomes 0.0083 / (4 X 0.0475) = 4.4% instead of 9.1%. The point is that small changes in cycle time may have large benefits.

Small modifications of other ‘‘rigid facts’’ can be beneficial.

Consider element sharing. That is, operators / station need not be 1.0. One possibility is more than

1 operator / station. Two operators / station yields 2.0 operators / station. Three operators / two stations

yields 1.5 operators / station. This permits a cycle time that is less than an element time. For example,

with 2 operators / station, each would do every other unit.

Get fewer than 1 operator / station by having operators walk between stations or having work done

off-line (i.e., using buffers). Also, operators from adjacent stations can share elements. For example,

station D does half of element 16 and 17 and station E does half of element 16 and 17.

Remember that cycle times are not fixed. We assumed a cycle time of 0.05 hr (i.e., the line runs

1000 hr or 1000 / 8 = 125 days). As pointed out above, it is more efficient to have cycle time of

0.0475 hr (i.e., 20,000 units X 0.0475 = 950 hr = 950/8 = 118.75 days). What is the best com- bination of setup cost, balance delay cost, and inventory carrying cost?

Elements can be redefined. For example, elements 16, 17, and 18 may be redefined to eliminate element 17 by allocating all of 17 to element 16 or to element 18 or to allocate a portion to element 16 or 18.

Reconsider the allocation of elements to subassemblies and assembly. For example, a nameplate might be added at a subassembly instead of at the assembly station.