PHYSICAL TASKS:OCCUPATIONAL BIOMECHANICS

By -

OCCUPATIONAL BIOMECHANICS

Definitions

As reviewed by Karwowski (1992), occupational biomechanics is a ‘‘study of the physical interaction of workers with their tools, machines and materials so as to enhance the worker’s performance while minimizing the risk of future musculoskeletal disorders’’ (Chaffin et al. 1999). There are six meth- odological areas, or contributing disciplines, important to the development of current knowledge in biomechanics:

1. Kinesiology, or study of human movement, which includes kinematics and kinetics

2. Biomechanical modeling methods, which refer to the forces acting on the human body while a worker is performing well-defined and rather common manual task

3. Mechanical work-capacity evaluation methods in relation to physical capacity of the worker and job demands

4. Bioinstrumentation methods (performance data acquisition and analysis)

5. Classification and time-prediction methods that allow for detailed time analysis of the human work activities and implementation of biomechanics principles to fit the workplace to the worker

Principles of Mechanics

Biomechanics considers safety and health implications of mechanics, or the study of the action of forces, for the human body (its anatomical and physiological properties) in motion (at work) and at rest. Mechanics, which is based on Newtonian physics, consists of two main areas: statics or the study of the human body at rest or in equilibrium, and dynamics or the study of the human body in motion. Dynamics is further subdivided into two main parts, kinematics and kinetics. Kinematics is concerned with the geometry of motion, including the relationships among displacements, velocities, and accelerations in both translational and rotational movements, without regard to the forces in- volved. Kinetics, on the other hand, is concerned with forces that act to produce the movements.

The types of forces acting on the human body at any given time are gravitational forces, external forces and ground reaction forces, and muscle forces (Winter 1979). Gravitational forces act down- ward, through the center of mass of body segments. The external forces are due to the body segment weights and external workload. The forces generated by the muscles are usually expressed as net muscle moments acting upon given joints. It should be noted that body (segment) weight is a (grav- itational) force, while body mass is a measure of inertia.

Biomechanical Analysis

Static Analysis

Static analysis requires consideration of forces and moments of force acting on the body at rest (static equilibrium). A magnitude of the moment of force at the point of rotation is equal to the product of force and the perpendicular distance from the force action line to that point. The moment (M) equals force (F) times moment arm (d), with unit of measurement (N·m). The static analysis ignores the effects of accelerations, momentum, and friction and is adequate only for analysis of static postures.

The body will be in a static equilibrium state when at rest or dynamic equilibrium when in motion with constant velocity. The translational equilibrium (first condition) of the body (segment) is present when the vector sum of all the forces acting on a body simultaneously is zero ("LF 0). The rotational equilibrium (second condition) of the body is present when the sum of moments about joint is zero ("LM 0). In other words, for the body to be at rest (zero velocity), the sum of all clockwise moments must be equal to the sum of all counterclockwise moments.

6.3.2. Lever Systems

Skeletal muscles of the human body produce movements of the bones about the joints by pulling at their anatomical attachments on the bones across the joints in order to counteract the external forces. This is possible due to three types of lever systems, composed of bones that serve as levers and joints that serve as points of pivot or fulcrums. The lever system consists of an effort force and the resistance force acting at different locations and distances with respect to the fulcrum. The force arm

Physical Tasks Analysis, Design, and-0030

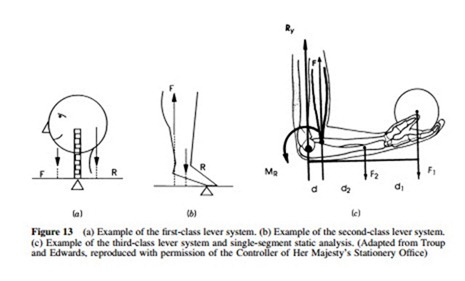
and the resistance arm are defined as the distance from the fulcrum to the effort force or resistance force, respectively. Mechanical advantage (MA) of the lever system is defined as the ratio between the force arm distance (dƒ) and the resistance arm distance (dr) where MA dƒ / dr.

In the first class of lever systems, the fulcrum is located between the effort and resistance. Ex- amples include the triceps muscle action of the ulna when the arm is abducted and held over the head, and the splenium muscles, acting to extend the head across the atlanto-occipital joints (Williams and Lissner 1977). The second class of lever systems is one where resistance is located between the fulcrum and the effort, providing for mechanical advantage greater than one. An example of such a lever system is the distribution of forces in the lower leg when raising one’s heel off the ground (see Figure 13). In the third class of lever systems, the effort is located between the fulcrum and the resistance, and consequently the mechanical advantage is always less than one, that is, to balance the resistance, the magnitude of effort must be greater than the magnitude of resistance. Many bone lever systems in the human body, for example, the system involved in forearm flexion as illustrated in Figure 13(c), are third-class systems.

Comments

Post a Comment

Popular posts from this blog

DUALITY THEORY:THE ESSENCE OF DUALITY THEORY

By -
Image
THE ESSENCE OF DUALITY THEORY Given our standard form for the primal problem at the left (perhaps after conversion from another form), its dual problem has the form shown to the right. Thus, with the primal problem in maximizatio n form, the dual problem is in minimization form instead. Furthermore, the dual problem uses exactly the same pa r amete r s as the primal problem, but in different locations, as summarized below. 1. The coefficients in the objective function of the primal problem are the right-hand sides of the functional constraints in the dual problem. 2. The right-hand sides of the functional constraints in the primal problem are the coef- ficients in the objective function of the dual problem. 3. The coefficients of a variable in the functional constraints of the primal problem are the coefficients in a functional constraint of the dual problem. To highlight the comparison, now look at these same two problems in matrix notation (as introduced at the beginn...
Read more

NETWORK OPTIMIZATION MODELS:THE MINIMUM SPANNING TREE PROBLEM

By -
Image
THE MINIMUM SPANNING TREE PROBLEM The minimum spanning tree problem bears some similarities to the main version of the shortest-path problem presented in the preceding section. In both cases, an undi r ecte d and connected network is being considered, where the given information includes some mea- sure of the positive length (distance, cost, time, etc.) associated with each link. Both problems also involve choosing a set of links that have the shortest total length among all sets of links that satisfy a certain property. For the shortest-path problem, this property is that the chosen links must provide a path between the origin and the destination. For the minimum spanning tree problem, the required property is that the chosen links must provide a path between ea c h pair of nodes. The minimum spanning tree problem can be summarized as follows: 1. You are given the nodes of a network but not the links. Instead, you are given the po- tential links and the positive length for each ...
Read more

INTEGER PROGRAMMING:THE BRANCH-AND-CUT APPROACH TO SOLVING BIP PROBLEMS

By -
TH E BRANCH-AND-CUT APPROACH TO SOLVING BIP PROBLEMS Integer programming has been an especially exciting area of OR since the mid-1980s be- cause of the dramatic progress being made in its solution methodology. Background To place this progress into perspective, consider the historical background. One big break- through had come in the 1960s and early 1970s with the development and refinement of the branch-and-bound approach. But then the state of the art seemed to hit a plateau. Rel- atively small problems (well under 100 variables) could be solved very efficiently, but even a modest increase in problem size might cause an explosion in computation time be- yond feasible limits. Little progress was being made in overcoming this exponential growth in computation time as the problem size was increased. Many important problems arising in practice could not be solved. Then came the next breakthrough in the mid-1980s, with the introduction of the b r an c h- and-cu t approach to sol...
Read more