An Example with a Dummy Source

An Example with a Dummy Source

METRO WATER DISTRICT is an agency that administers water distribution in a large geographic region. The region is fairly arid, so the district must purchase and bring in water from outside the region. The sources of this imported water are the Colombo, Sacron, and Calorie rivers. The district then resells the water to users in the region. Its main customers are the water departments of the cities of Berdoo, Los Devils, San Go, and Hollyglass.

It is possible to supply any of these cities with water brought in from any of the three rivers, with the exception that no provision has been made to supply Hollyglass with Calo- rie River water. However, because of the geographic layouts of the aqueducts and the cities in the region, the cost to the district of supplying water depends upon both the source of the water and the city being supplied. The variable cost per acre foot of water (in tens of dollars) for each combination of river and city is given in Table 9.10. Despite these variations, the price per acre foot charged by the district is independent of the source of the water and is the same for all cities.

The management of the district is now faced with the problem of how to allocate the available water during the upcoming summer season. In units of 1 million acre feet, the amounts available from the three rivers are given in the rightmost column of Table 9.10. The district is committed to providing a certain minimum amount to meet the essential needs of each city (with the exception of San Go, which has an independent source of water), as shown in the minimum needed row of the table. The requested row indicates that Los Devils desires no more than the minimum amount, but that Berdoo would like to buy as much as 20 more, San Go would buy up to 30 more, and Hollyglass will take as much as it can get.

Management wishes to allocate all the available water from the three rivers to the four cities in such a way as to at least meet the essential needs of each city while mini- mizing the total cost to the district.

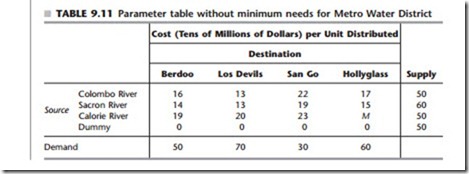
Formulation. Table 9.10 already is close to the proper form for a parameter table, with the rivers being the sources and the cities being the destinations. However, the one basic difficulty is that it is not clear what the demands at the destinations should be. The amount to be received at each destination (except Los Devils) actually is a decision variable, with both a lower bound and an upper bound. This upper bound is the amount requested un- less the request exceeds the total supply remaining after the minimum needs of the other cities are met, in which case this remaining supply becomes the upper bound. Thus, in- satiably thirsty Hollyglass has an upper bound of

(50 + 60 + 50) - (30 + 70 + 0) = 60.

Unfortunately, just like the other numbers in the parameter table of a transportation problem, the demand quantities must be constants, not bounded decision variables. To

begin resolving this difficulty, temporarily suppose that it is not necessary to satisfy the minimum needs, so that the upper bounds are the only constraints on amounts to be al- located to the cities. In this circumstance, can the requested allocations be viewed as the demand quantities for a transportation problem formulation? After one adjustment, yes! (Do you see already what the needed adjustment is?)

The situation is analogous to Northern Airplane Co.’s production scheduling problem, where there was excess supply capacity. Now there is excess demand capacity. Con- sequently, rather than introducing a dummy destination to “receive” the unused supply capacity, the adjustment needed here is to introduce a dummy source to “send” the un- used demand capacity. The imaginary supply quantity for this dummy source would be the amount by which the sum of the demands exceeds the sum of the real supplies:

(50 + 70 + 30 + 60) - (50 + 60 + 50) = 50.

This formulation yields the parameter table shown in Table 9.11, which uses units of million acre feet and tens of millions of dollars. The cost entries in the dummy row are zero because there is no cost incurred by the fictional allocations from this dummy source. On the other hand, a huge unit cost of M is assigned to the Calorie River–Hollyglass spot. The reason is that Calorie River water cannot be used to supply Hollyglass, and assign- ing a cost of M will prevent any such allocation.

Now let us see how we can take each city’s minimum needs into account in this kind of formulation. Because San Go has no minimum need, it is all set. Similarly, the for- mulation for Hollyglass does not require any adjustments because its demand (60) ex- ceeds the dummy source’s supply (50) by 10, so the amount supplied to Hollyglass from the real sources will be at least 10 in any feasible solution. Consequently, its minimum need of 10 from the rivers is guaranteed. (If this coincidence had not occurred, Hollyglass would need the same adjustments that we shall have to make for Berdoo.)

Los Devils’ minimum need equals its requested allocation, so its entire demand of 70 must be filled from the real sources rather than the dummy source. This requirement calls for the Big M method! Assigning a huge unit cost of M to the allocation from the dummy source to Los Devils ensures that this allocation will be zero in an optimal solution.

Finally, consider Berdoo. In contrast to Hollyglass, the dummy source has an ade- quate (fictional) supply to “provide” at least some of Berdoo’s minimum need in addition to its extra requested amount. Therefore, since Berdoo’s minimum need is 30, adjustments must be made to prevent the dummy source from contributing more than 20 to Berdoo’s total demand of 50. This adjustment is accomplished by splitting Berdoo into two desti- nations, one having a demand of 30 with a unit cost of M for any allocation from the dummy source and the other having a demand of 20 with a unit cost of zero for the dummy source allocation. This formulation gives the final parameter table shown in Table 9.12.

Generalizations of the Transportation Problem

Even after the kinds of reformulations illustrated by the two preceding examples, some problems involving the distribution of units from sources to destinations fail to satisfy the model for the transportation problem. One reason may be that the distribution does not go directly from the sources to the destinations but instead passes through transfer points along the way. The Distribution Unlimited Co example in Sec. 3.4 (see Fig. 3.13) illus- trates such a problem. In this case, the sources are the two factories and the destinations are the two warehouses. However, a shipment from a particular factory to a particular warehouse may first get transferred at a distribution center, or even at the other factory or the other warehouse, before reaching its destination. The unit shipping costs differ for these different shipping lanes. Furthermore, there are upper limits on how much can be shipped through some of the shipping lanes. Although it is not a transportation problem, this kind of problem still is a special type of linear programming problem, called the min- imum cost flow problem, that will be discussed in Sec. 10.6. The network simplex method described in Sec. 10.7 provides an efficient way of solving minimum cost flow problems. A minimum cost flow problem that does not impose any upper limits on how much can be shipped through the shipping lanes is referred to as a transshipment problem. Section 23.1 on the book’s website is devoted to discussing transshipment problems.

In other cases, the distribution may go directly from sources to destinations, but other assumptions of the transportation problem may be violated. The cost assumption will be violated if the cost of distributing units from any particular source to any particular destination is a nonlinear function of the number of units distributed. The requirements assumption will be violated if either the supplies from the sources or the demands at the destinations are not fixed. For example, the final demand at a destination may not become known until after the units have arrived and then a nonlinear cost is incurred if the amount received deviates from the final demand. If the supply at a source is not fixed, the cost of producing the amount supplied may be a nonlinear function of this amount. For example, a fixed cost may be part of the cost associated with a decision to open up a new source. Considerable research has been done to generalize the transportation problem and its solution procedure in these kinds of directions.2

2For example, see K. Holmberg and H. Tuy: “A Production-Transportation Problem with Stochastic Demand and Concave Production Costs,” Mathematical Programming Series A, 85: 157–179, 1999.