DYNAMIC PROGRAMMING:A PROTOTYPE EXAMPLE FOR DYNAMIC PROGRAMMING

A PROTOTYPE EXAMPLE FOR DYNAMIC PROGRAMMING

EXAMPLE 1 The Stagecoach Problem

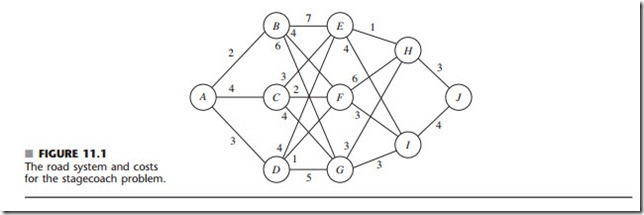
The STAGECOACH PROBLEM is a problem specially constructed1 to illustrate the features and to introduce the terminology of dynamic programming. It concerns a mythical fortune seeker in Missouri who decided to go west to join the gold rush in California during the mid-19th century. The journey would require traveling by stagecoach through unsettled country where there was serious danger of attack by marauders. Although his starting point and destination were fixed, he had considerable choice as to which states (or territories that subsequently became states) to travel through en route. The possible routes are shown in Fig. 11.1, where each state is represented by a circled letter and the direction of travel is always from left to right in the diagram. Thus, four stages (stage- coach runs) were required to travel from his point of embarkation in state A (Missouri) to his destination in state J (California).

This fortune seeker was a prudent man who was quite concerned about his safety. After some thought, he came up with a rather clever way of determining the safest route. Life

insurance policies were offered to stagecoach passengers. Because the cost of the policy for taking any given stagecoach run was based on a careful evaluation of the safety of that run, the safest route should be the one with the cheapest total life insurance policy.

The cost for the standard policy on the stagecoach run from state i to state j, which will be denoted by cij, is

We shall now focus on the question of which route minimizes the total cost of the policy.

Solving the Problem

First note that the shortsighted approach of selecting the cheapest run offered by each suc- cessive stage need not yield an overall optimal decision. Following this strategy would give the route A --- B --- F --- I --- J, at a total cost of 13. However, sacrificing a little on one stage may permit greater savings thereafter. For example, A --- D --- F is cheaper overall than A --- B --- F.

One possible approach to solving this problem is to use trial and error.2 However, the number of possible routes is large (18), and having to calculate the total cost for each route is not an appealing task.

Fortunately, dynamic programming provides a solution with much less effort than exhaustive enumeration. (The computational savings are enormous for larger versions of this problem.) Dynamic programming starts with a small portion of the original problem and finds the optimal solution for this smaller problem. It then gradually enlarges the problem, finding the current optimal solution from the preceding one, until the original problem is solved in its entirety.

2This problem also can be formulated as a shortest-path problem (see Sec. 10.3), where costs here play the role of distances in the shortest-path problem. The algorithm presented in Sec. 10.3 actually uses the philosophy of dynamic programming. However, because the present problem has a fixed number of stages, the dynamic pro- gramming approach presented here is even better.

For the stagecoach problem, we start with the smaller problem where the fortune seeker has nearly completed his journey and has only one more stage (stagecoach run) to go. The obvious optimal solution for this smaller problem is to go from his current state (whatever it is) to his ultimate destination (state J ). At each subsequent iteration, the problem is enlarged by increasing by 1 the number of stages left to go to complete the journey. For this enlarged problem, the optimal solution for where to go next from each possible state can be found relatively easily from the results obtained at the preceding iteration. The details involved in implementing this approach follow.

Formulation. Let the decision variables xn (n = 1, 2, 3, 4) be the immediate destina- tion on stage n (the nth stagecoach run to be taken). Thus, the route selected is A --- x1 --- x2 --- x3 --- x4, where x4 = J.

When the fortune seeker has two more stages to go (n = 3), the solution procedure requires a few calculations. For example, suppose that the fortune seeker is in state F. Then, as depicted below, he must next go to either state H or I at an immediate cost of cF,H = 6 or cF,I = 3, respectively. If he chooses state H, the minimum additional cost af- ter he reaches there is given in the preceding table as f 4*(H ) = 3, as shown above the H node in the diagram. Therefore, the total cost for this decision is 6 + 3 = 9. If he chooses state I instead, the total cost is 3 + 4 = 7, which is smaller. Therefore, the optimal choice is this latter one, x3* = I, because it gives the minimum cost f 3*(F ) = 7.

3Because this procedure involves moving backward stage by stage, some writers also count n backward to denote the number of remaining stages to the destination. We use the more natural forward counting for greater simplicity.

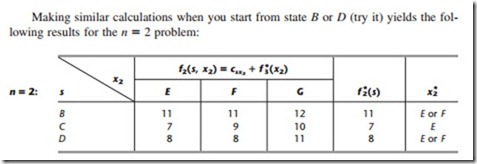
In the first and third rows of this table, note that E and F tie as the minimizing value of x2, so the immediate destination from either state B or D should be x2* = E or F.

Moving to the first-stage problem (n = 1), with all four stages to go, we see that the calculations are similar to those just shown for the second-stage problem (n = 2), except now there is just one possible starting state s = A, as depicted below.

solution of the stagecoach problem. Each arrow shows an optimal policy decision (the best immediate destination) from that state, where the number by the state is the resulting cost from there to the end. Following the boldface arrows from A to J gives the three optimal solutions (the three routes giving the arrows (and the resulting cost) comes from one row in one of the other tables in just the same way.

You will see in the next section that the special terms describing the particular con- text of this problem—stage, state, and policy—actually are part of the general terminol- ogy of dynamic programming with an analogous interpretation in other contexts.