DUALITY THEORY:PRIMAL–DUAL RELATIONSHIPS

PRIMAL–DUAL RELATIONSHIPS

Because the dual problem is a linear programming problem, it also has corner-point so- lutions. Furthermore, by using the augmented form of the problem, we can express these corner-point solutions as basic solutions. Because the functional constraints have the> form, this augmented form is obtained by subtracting the surplus (rather than adding the slack) from the left-hand side of each constraint j ( j = 1, 2, . . . , n).2 This surplus is

Thus, zj-cj plays the role of the surplus variable for constraint j (or its slack variable if the constraint is multiplied through by -1). Therefore, augmenting each corner-point so- lution ( y1, y2, . . . , ym) yields a basic solution ( y1, y2, . . . , ym , z1 - c1, z2 - c2, . . . , zn - cn) by using this expression for zj - cj. Since the augmented form of the dual problem has n functional constraints and n + m variables, each basic solution has n basic variables and m nonbasic variables. (Note how m and n reverse their previous roles here because, as Table 6.3 indicates, dual constraints correspond to primal variables and dual variables correspond to primal constraints.)

2You might wonder why we do not also introduce artificial variables into these constraints as discussed in Sec. 4.6. The reason is that these variables have no purpose other than to change the feasible region tem- porarily as a convenience in starting the simplex method. We are not interested now in applying the simplex method to the dual problem, and we do not want to change its feasible region.

Complementary Basic Solutions

One of the important relationships between the primal and dual problems is a direct cor- respondence between their basic solutions. The key to this correspondence is row 0 of the simplex tableau for the primal basic solution, such as shown in Table 6.4 or 6.5. Such a row 0 can be obtained for any primal basic solution, feasible or not, by using the formu- las given in the bottom part of Table 5.8.

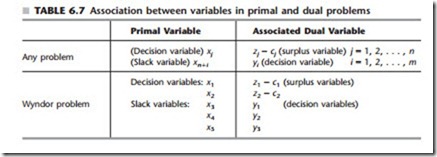
Note again in Tables 6.4 and 6.5 how a complete solution for the dual problem (includ- ing the surplus variables) can be read directly from row 0. Thus, because of its coefficient in row 0, each variable in the primal problem has an associated variable in the dual problem, as summarized in Table 6.7, first for any problem and then for the Wyndor problem.

A key insight here is that the dual solution read from row 0 must also be a basic so- lution! The reason is that the m basic variables for the primal problem are required to have a coefficient of zero in row 0, which thereby requires the m associated dual variables to be zero, i.e., nonbasic variables for the dual problem. The values of the remaining n (ba- sic) variables then will be the simultaneous solution to the system of equations given at the beginning of this section. In matrix form, this system of equations is z - c = yA - c, and the fundamental insight of Sec. 5.3 actually identifies its solution for z - c and y as being the corresponding entries in row 0.

Because of the symmetry property quoted in Sec. 6.1 (and the direct association be- tween variables shown in Table 6.7), the correspondence between basic solutions in the primal and dual problems is a symmetric one. Furthermore, a pair of complementary ba- sic solutions has the same objective function value, shown as W in Table 6.4.

Let us now summarize our conclusions about the correspondence between primal and dual basic solutions, where the first property extends the complementary solutions prop- erty of Sec. 6.1 to the augmented forms of the two problems and then to any basic solu- tion (feasible or not) in the primal problem.

Complementary basic solutions property: Each basic solution in the primal problem has a complementary basic solution in the dual problem, where their respective objective function values (Z and W ) are equal. Given row 0 of the sim- plex tableau for the primal basic solution, the complementary dual basic solution (y, z - c) is found as shown in Table 6.4.

The next property shows how to identify the basic and nonbasic variables in this com- plementary basic solution.

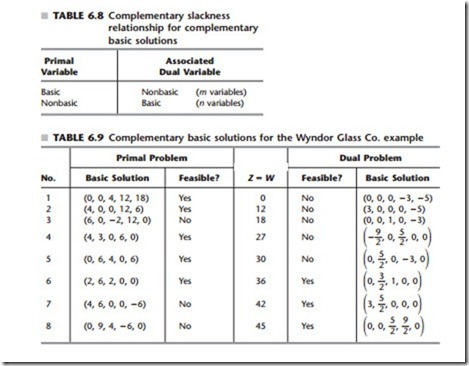
Complementary slackness property: Given the association between variables in Table 6.7, the variables in the primal basic solution and the complementary dual basic solution satisfy the complementary slackness relationship shown in Table 6.8. Furthermore, this relationship is a symmetric one, so that these two basic solutions are complementary to each other.

The reason for using the name complementary slackness for this latter property is that it says (in part) that for each pair of associated variables, if one of them has slack in its nonnegativity constraint (a basic variable > 0), then the other one must have no slack (a nonbasic variable = 0). We mentioned in Sec. 6.2 that this property has a useful economic interpretation for linear programming problems.

Example. To illustrate these two properties, again consider the Wyndor Glass Co. prob- lem of Sec. 3.1. All eight of its basic solutions (five feasible and three infeasible) are shown in Table 6.9. Thus, its dual problem (see Table 6.1) also must have eight basic so- lutions, each complementary to one of these primal solutions, as shown in Table 6.9.

The three BF solutions obtained by the simplex method for the primal problem are the first, fifth, and sixth primal solutions shown in Table 6.9. You already saw in Table 6.5 how the complementary basic solutions for the dual problem can be read directly from row 0, starting with the coefficients of the slack variables and then the original variables. The other dual basic solutions also could be identified in this way by constructing row 0 for each of the other primal basic solutions, using the formulas given in the bottom part of Table 5.8.

Alternatively, for each primal basic solution, the complementary slackness property can be used to identify the basic and nonbasic variables for the complementary dual ba- sic solution, so that the system of equations given at the beginning of the section can be solved directly to obtain this complementary solution. For example, consider the next-to- last primal basic solution in Table 6.9, (4, 6, 0, 0, -6). Note that x1, x2, and x5 are basic variables, since these variables are not equal to 0. Table 6.7 indicates that the associated dual variables are (z1 - c1), (z2 - c2), and y3. Table 6.8 specifies that these associated dual variables are nonbasic variables in the complementary basic solution, so

Finally, notice that Table 6.9 demonstrates that (0, 3, 1, 0, 0) is the optimal solution for the dual problem, because it is the basic feasible solution with minimal W (36).

Relationships between Complementary Basic Solutions

We now turn our attention to the relationships between complementary basic solutions, beginning with their feasibility relationships. The middle columns in Table 6.9 provide some valuable clues. For the pairs of complementary solutions, notice how the yes or no answers on feasibility also satisfy a complementary relationship in most cases. In partic- ular, with one exception, whenever one solution is feasible, the other is not. (It also is possible for neither solution to be feasible, as happened with the third pair.) The one ex- ception is the sixth pair, where the primal solution is known to be optimal. The explana- tion is suggested by the Z = W column. Because the sixth dual solution also is optimal (by the complementary optimal solutions property), with W = 36, the first five dual so- lutions cannot be feasible because W < 36 (remember that the dual problem objective is to minimize W ). By the same token, the last two primal solutions cannot be feasible be- cause Z > 36.

This explanation is further supported by the strong duality property that optimal primal and dual solutions have Z = W.

Next, let us state the extension of the complementary optimal solutions property of Sec. 6.1 for the augmented forms of the two problems.

Complementary optimal basic solutions property: An optimal basic solution in the primal problem has a complementary optimal basic solution in the dual problem, where their respective objective function values (Z and W ) are equal. Given row 0 of the simplex tableau for the optimal primal solution, the comple- mentary optimal dual solution (y*, z* - c) is found as shown in Table 6.4.

To review the reasoning behind this property, note that the dual solution (y*, z* - c) must be feasible for the dual problem because the condition for optimality for the pri- mal problem requires that all these dual variables (including surplus variables) be non- negative. Since this solution is feasible, it must be optimal for the dual problem by the weak duality property (since W = Z, so y*b = cx* where x* is optimal for the primal problem).

Basic solutions can be classified according to whether they satisfy each of two con- ditions. One is the condition for feasibility, namely, whether all the variables (including slack variables) in the augmented solution are nonnegative. The other is the condition for optimality, namely, whether all the coefficients in row 0 (i.e., all the variables in the complementary basic solution) are nonnegative. Our names for the different types of basic solutions are summarized in Table 6.10. For example, in Table 6.9, primal basic

Given these definitions, the general relationships between complementary basic so- lutions are summarized in Table 6.11. The resulting range of possible (common) values for the objective functions (Z = W ) for the first three pairs given in Table 6.11 (the last pair can have any value) is shown in Fig. 6.1. Thus, while the simplex method is dealing

directly with suboptimal basic solutions and working toward optimality in the primal problem, it is simultaneously dealing indirectly with complementary superoptimal solutions and working toward feasibility in the dual problem. Conversely, it sometimes is more con- venient (or necessary) to work directly with superoptimal basic solutions and to move to- ward feasibility in the primal problem, which is the purpose of the dual simplex method described in Sec. 8.1.

The third and fourth columns of Table 6.11 introduce two other common terms that are used to describe a pair of complementary basic solutions. The two solutions are said to be primal feasible if the primal basic solution is feasible, whereas they are called dual feasible if the complementary dual basic solution is feasible for the dual problem. Using this terminology, the simplex method deals with primal feasible solutions and strives to- ward achieving dual feasibility as well. When this is achieved, the two complementary basic solutions are optimal for their respective problems.

These relationships prove very useful, particularly in sensitivity analysis, as you will see in the next chapter.