NETWORK OPTIMIZATION MODELS:THE MINIMUM COST FLOW PROBLEM

THE MINIMUM COST FLOW PROBLEM

The minimum cost flow problem holds a central position among network optimization mod- els, both because it encompasses such a broad class of applications and because it can be solved extremely efficiently. Like the maximum flow problem, it considers flow through a network with limited arc capacities. Like the shortest-path problem, it considers a cost (or distance) for flow through an arc. Like the transportation problem or assignment problem of Chap. 9, it can consider multiple sources (supply nodes) and multiple destinations (demand nodes) for the flow, again with associated costs. In fact, all four of these previously studied problems are special cases of the minimum cost flow problem, as we will demonstrate shortly.

The reason that the minimum cost flow problem can be solved so efficiently is that it can be formulated as a linear programming problem so it can be solved by a stream- lined version of the simplex method called the network simplex method. We describe this algorithm in the next section.

The minimum cost flow problem is described below:

1. The network is a directed and connected network.

2. At least one of the nodes is a supply node.

3. At least one of the other nodes is a demand node.

4. All the remaining nodes are transshipment nodes.

5. Flow through an arc is allowed only in the direction indicated by the arrowhead, where the maximum amount of flow is given by the capacity of that arc. (If flow can occur in both directions, this would be represented by a pair of arcs pointing in opposite directions.)

6. The network has enough arcs with sufficient capacity to enable all the flow generated at the supply nodes to reach all the demand nodes.

7. The cost of the flow through each arc is proportional to the amount of that flow, where the cost per unit flow is known.

8. The objective is to minimize the total cost of sending the available supply through the network to satisfy the given demand. (An alternative objective is to maximize the to- tal profit from doing this.)

Some Applications

Probably the most important kind of application of minimum cost flow problems is to the operation of a company’s distribution network. As summarized in the first row of Table 10.3, this kind of application always involves determining a plan for shipping goods from its sources (factories, etc.) to intermediate storage facilities (as needed) and then on to the customers.

For some applications of minimum cost flow problems, all the transshipment nodes are processing facilities rather than intermediate storage facilities. This is the case for

An Application Vignette

An especially challenging problem encountered daily by any major airline company is how to compensate effec- tively for disruptions in the airline's flight schedules. Bad weather can disrupt flight arrivals and departures; so can mechanical problems. Each delay or cancellation involv- ing a particular airplane can then cause subsequent delays or cancellations because that airplane is not available on time for its next scheduled flights.

Such delays or cancellations may require both reas- signing crews to flights and readjusting the plans for which airplanes will be used to fly the respective flights. The application vignette in Sec. 2.2 describes how Conti- nental Airlines led the way in applying operations research to the problem of quickly reassigning crews to flights in the most cost-effective manner. However, a dif- ferent approach is needed to address the problem of quickly reassigning airplanes to flights.

An airline has two primary ways of reassigning air- planes to flights to compensate for delays or cancella- tions. One is to swap aircraft so that an airplane scheduled for a later flight can take the place of the delayed or can- celed airplane. The other is to use a spare airplane (often after flying it in) to replace the delayed or canceled

airplane. However, it is a real challenge to quickly make good decisions of these types when a considerable num- ber of delays or cancellations occur throughout the day.

United Airlines has led the way in applying opera- tions research to this problem. This is done by formulat- ing and solving the problem as a minimum-cost flow problem where each node in the network represents an airport and each arc represents the route of a flight. The objective of the model then is to keep the airplanes flow- ing through the network in a way that minimizes the cost incurred by having delays or cancellations. When a status monitor subsystem alerts an operations controller of impending delays or cancellations, the controller pro- vides the necessary input into the model and then solves it in order to provide the updated operating plan in a mat- ter of minutes. This application of the minimum-cost flow problem has resulted in reducing passenger delays by about 50 percent.

Source: A. Rakshit, N. Krishnamurthy, and G. Yu: “System Operations Advisor: A Real-Time Decision Support System for Managing Airline Operations at United Airlines,” Interfaces, 26(2): 50–58, Mar.–Apr. 1996. (A link to this article is provided on our website, www.mhhe.com/hillier.)

solid waste management, as indicated in the second row of Table 10.3. Here, the flow of materials through the network begins at the sources of the solid waste, then goes to the facilities for processing these waste materials into a form suitable for landfill, and then sends them on to the various landfill locations. However, the objective still is to deter- mine the flow plan that minimizes the total cost, where the cost now is for both shipping and processing.

In other applications, the demand nodes might be processing facilities. For example, in the third row of Table 10.3, the objective is to find the minimum cost plan for obtain- ing supplies from various possible vendors, storing these goods in warehouses (as needed), and then shipping the supplies to the company’s processing facilities (factories, etc.). Since the total amount that could be supplied by all the vendors is more than the company needs, the network includes a dummy demand node that receives (at zero cost) all the unused supply capacity at the vendors.

The next kind of application in Table 10.3 (coordinating product mixes at plants) il- lustrates that arcs can represent something other than a shipping lane for a physical flow of materials. This application involves a company with several plants (the supply nodes) that can produce the same products but at different costs. Each arc from a supply node represents the production of one of the possible products at that plant, where this arc leads to the transshipment node that corresponds to this product. Thus, this transship- ment node has an arc coming in from each plant capable of producing this product, and then the arcs leading out of this node go to the respective customers (the demand nodes) for this product. The objective is to determine how to divide each plant’s production capacity among the products so as to minimize the total cost of meeting the demand for the various products.

The last application in Table 10.3 (cash flow management) illustrates that different nodes can represent some event that occurs at different times. In this case, each supply node represents a specific time (or time period) when some cash will become available to the company (through maturing accounts, notes receivable, sales of securities, borrowing, etc.). The supply at each of these nodes is the amount of cash that will become available then. Similarly, each demand node represents a specific time (or time period) when the company will need to draw on its cash reserves. The demand at each such node is the amount of cash that will be needed then. The objective is to maximize the company’s income from investing the cash between each time it becomes available and when it will be used. There- fore, each transshipment node represents the choice of a specific short-term investment option (e.g., purchasing a certificate of deposit from a bank) over a specific time interval. The resulting network will have a succession of flows representing a schedule for cash becoming available, being invested, and then being used after the maturing of the investment.

Formulation of the Model

Consider a directed and connected network where the n nodes include at least one sup- ply node and at least one demand node. The decision variables are

The first summation in the node constraints represents the total flow out of node i, whereas the second summation represents the total flow into node i, so the difference is the net flow generated at this node.

The pattern of the coefficients in these node constraints is a key characteristic of min- imum cost flow problems. It is not always easy to recognize a minimum cost flow prob- lem, but formulating (or reformulating) a problem so that its constraint coefficients have this pattern is a good way of doing so. This then enables solving the problem extremely efficiently by the network simplex method.

In some applications, it is necessary to have a lower bound Lij > 0 for the flow through each arc i --- j. When this occurs, use a translation of variables xi'j = xij - Lij, with xi'j + Lij substituted for xij throughout the model, to convert the model back to the above format with nonnegativity constraints.

It is not guaranteed that the problem actually will possess feasible solutions, depending partially upon which arcs are present in the network and their arc capacities. However, for a reasonably designed network, the main condition needed is the following:

Feasible solutions property: A necessary condition for a minimum cost flow problem to have any feasible solutions is that

That is, the total flow being generated at the supply nodes equals the total flow being absorbed at the demand nodes.

If the values of bi provided for some application violate this condition, the usual inter- pretation is that either the supplies or the demands (whichever are in excess) actually represent upper bounds rather than exact amounts. When this situation arose for the trans- portation problem in Sec. 9.1, either a dummy destination was added to receive the ex- cess supply or a dummy source was added to send the excess demand. The analogous step now is that either a dummy demand node should be added to absorb the excess sup- ply (with cij = 0 arcs added from every supply node to this node) or a dummy supply node should be added to generate the flow for the excess demand (with cij = 0 arcs added from this node to every demand node).

For many applications, bi and uij will have integer values, and implementation will require that the flow quantities xij also be integer. Fortunately, just as for the transporta- tion problem, this outcome is guaranteed without explicitly imposing integer constraints on the variables because of the following property.

Integer solutions property: For minimum cost flow problems where every bi and uij have integer values, all the basic variables in every basic feasible (BF) solution (including an optimal one) also have integer values.

An Example

Figure 10.12 shows an example of a minimum cost flow problem. This network actually is the distribution network for the Distribution Unlimited Co. problem presented in Sec.

3.4 (see Fig. 3.13). The quantities given in Fig. 3.13 provide the values of the bi, cij, and uij shown here. The bi values in Fig. 10.12 are shown in square brackets by the nodes, so the supply nodes (bi > 0) are A and B (the company’s two factories), the demand nodes (bi < 0) are D and E (two warehouses), and the one transshipment node (bi = 0) is C (a distribution center). The cij values are shown next to the arcs. In this example, all but two of the arcs have arc capacities exceeding the total flow generated (90), so uij = oo for all practical purposes. The two exceptions are arc A --- B, where uAB = 10, and arc C --- E, which has uCE = 80.

The linear programming model for this example is

Now note the pattern of coefficients for each variable in the set of five node constraints (the equality constraints). Each variable has exactly two nonzero coefficients, where one is +1 and the other is -1. This pattern recurs in every minimum cost flow problem, and it is this special structure that leads to the integer solutions property.

Another implication of this special structure is that (any) one of the node constraints is redundant. The reason is that summing all these constraint equations yields nothing but ze- ros on both sides (assuming feasible solutions exist, so the bi values sum to zero), so the negative of any one of these equations equals the sum of the rest of the equations. With just n - 1 nonredundant node constraints, these equations provide just n - 1 basic variables for a BF solution. In the next section, you will see that the network simplex method treats the xij ::: uij constraints as mirror images of the nonnegativity constraints, so the total number of basic variables is n - 1. This leads to a direct correspondence between the n - 1 arcs of a spanning tree and the n - 1 basic variables—but more about that story later.

Using Excel to Formulate and Solve Minimum Cost Flow Problems Excel provides a convenient way of formulating and solving small minimum cost flow problems like this one, as well as somewhat larger problems. Figure 10.13 shows how this can be done. The format is almost the same as displayed in Fig. 10.11 for a max- imum flow problem. One difference is that the unit costs (cij) now need to be included (in column G). Because bi values are specified for every node, net flow constraints are needed for all the nodes. However, only two of the arcs happen to need arc capacity

constraints. The objective cell TotalCost (D12) now gives the total cost of the flow (shipments) through the network (see its equation at the bottom of the figure), so the goal specified in Solver is to minimize this quantity. The changing cells Ship (D4:D10) in this spreadsheet show the optimal solution obtained after running Solver.

For much larger minimum cost flow problems, the network simplex method described in the next section provides a considerably more efficient solution procedure. It also is an attractive option for solving various special cases of the minimum cost flow problem out- lined below. This algorithm is commonly included in mathematical programming soft- ware packages.

We shall soon solve this same example by the network simplex method. However, let us first see how some special cases fit into the network format of the minimum cost flow problem.

Special Cases

The Transportation Problem. To formulate the transportation problem presented in Sec. 9.1 as a minimum cost flow problem, a supply node is provided for each source, as well as a demand node for each destination, but no transshipment nodes are included in the network. All the arcs are directed from a supply node to a demand node, where distributing xij units from source i to destination j corresponds to a flow of xij through arc i --- j. The cost cij per unit distributed becomes the cost cij per unit of flow. Since the transportation problem does not impose upper bound constraints on individual xij, all the uij = oo.

Using this formulation for the P & T Co. transportation problem presented in Table 9.2

yields the network shown in Fig. 9.2. The corresponding network for the general trans- portation problem is shown in Fig. 9.3.

The Assignment Problem. Since the assignment problem discussed in Sec. 9.3 is a special type of transportation problem, its formulation as a minimum cost flow problem fits into the same format. The additional factors are that (1) the number of supply nodes

equals the number of demand nodes, (2) bi = 1 for each supply node, and (3) bi = -1 for each demand node.

Figure 9.5 shows this formulation for the general assignment problem.

The Transshipment Problem. This special case actually includes all the general fea- tures of the minimum cost flow problem except for not having (finite) arc capacities. Thus, any minimum cost flow problem where each arc can carry any desired amount of flow is also called a transshipment problem.

For example, the Distribution Unlimited Co. problem shown in Fig. 10.13 would be a transshipment problem if the upper bounds on the flow through arcs A --- B and C --- E were removed.

Transshipment problems frequently arise as generalizations of transportation problems where units being distributed from each source to each destination can first pass through intermediate points. These intermediate points may include other sources and des- tinations, as well as additional transfer points that would be represented by transshipment nodes in the network representation of the problem. For example, the Distribution Un- limited Co. problem can be viewed as a generalization of a transportation problem with two sources (the two factories represented by nodes A and B in Fig. 10.13), two destinations (the two warehouses represented by nodes D and E ), and one additional intermedi- ate transfer point (the distribution center represented by node C ).

(The first section in Chap. 23 on the book’s website includes a further discussion of the transshipment problem.)

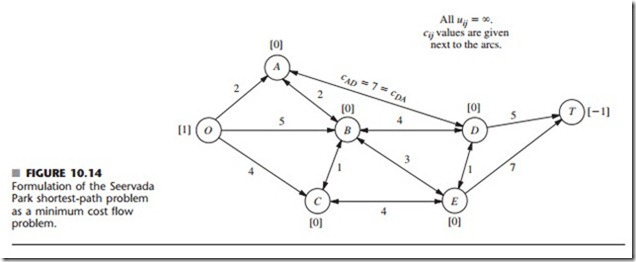
The Shortest-Path Problem. Now consider the main version of the shortest-path problem presented in Sec. 10.3 (finding the shortest path from one origin to one destina- tion through an undirected network). To formulate this problem as a minimum cost flow problem, one supply node with a supply of 1 is provided for the origin, one demand node with a demand of 1 is provided for the destination, and the rest of the nodes are trans- shipment nodes. Because the network of our shortest-path problem is undirected, whereas the minimum cost flow problem is assumed to have a directed network, we replace each link with a pair of directed arcs in opposite directions (depicted by a single line with arrowheads at both ends). The only exceptions are that there is no need to bother with arcs into the supply node or out of the demand node. The distance between nodes i and j be- comes the unit cost cij or cji for flow in either direction between these nodes. As with the preceding special cases, no arc capacities are imposed, so all uij = oo.

Figure 10.14 depicts this formulation for the Seervada Park shortest-path problem shown in Fig. 10.1, where the numbers next to the lines now represent the unit cost of flow in either direction.

The Maximum Flow Problem. The last special case we shall consider is the maxi- mum flow problem described in Sec. 10.5. In this case a network already is provided with one supply node (the source), one demand node (the sink), and various transshipment nodes, as well as the various arcs and arc capacities. Only three adjustments are needed to fit this problem into the format for the minimum cost flow problem. First, set cij = 0 for all existing arcs to reflect the absence of costs in the maximum flow problem. Sec- ond, select a quantity F, which is a safe upper bound on the maximum feasible flow through the network, and then assign a supply and a demand of F to the supply node and the demand node, respectively. (Because all other nodes are transshipment nodes, they au- tomatically have bi = 0.) Third, add an arc going directly from the supply node to the de- mand node and assign it an arbitrarily large unit cost of cij = M as well as an unlimited arc capacity (uij = oo). Because of this positive unit cost for this arc and the zero unit cost

for all the other arcs, the minimum cost flow problem will send the maximum feasible flow through the other arcs, which achieves the objective of the maximum flow problem.

Applying this formulation to the Seervada Park maximum flow problem shown in Fig. 10.6 yields the network given in Fig. 10.15, where the numbers given next to the original arcs are the arc capacities.

Final Comments. Except for the transshipment problem, each of these special cases has been the focus of a previous section in either this chapter or Chap. 9. When each was first presented, we talked about a special-purpose algorithm for solving it very efficiently. Therefore, it certainly is not necessary to reformulate these special cases to fit the format of the minimum cost flow problem in order to solve them. However, when a computer code is not readily available for the special-purpose algorithm, it is very reasonable to use the network simplex method instead. In fact, recent implementations of the network simplex method have become so powerful that it now provides an excellent alternative to the special-purpose algorithm.

The fact that these problems are special cases of the minimum cost flow problem is of interest for other reasons as well. One reason is that the underlying theory for the min- imum cost flow problem and for the network simplex method provides a unifying theory for all these special cases. Another reason is that some of the many applications of the minimum cost flow problem include features of one or more of the special cases, so it is important to know how to reformulate these features into the broader framework of the general problem.