INTEGER PROGRAMMING:A BRANCH-AND-BOUND ALGORITHM FOR MIXED INTEGER PROGRAMMING

A BRANCH-AND-BOUND ALGORITHM FOR MIXED INTEGER PROGRAMMING

We shall now consider the general MIP problem, where some of the variables (say, I of them) are restricted to integer values (but not necessarily just 0 and 1) but the rest are ordinary continuous variables. For notational convenience, we shall order the variables so that the first I variables are the integer-restricted variables. Therefore, the general form of the problem being considered is

(When I = n, this problem becomes the pure IP problem.)

We shall describe a basic branch-and-bound algorithm for solving this problem that, with a variety of refinements, has provided a standard approach to MIP. The structure of this algorithm was first developed by R. J. Dakin,9 based on a pioneering branch-and-bound algorithm by A. H. Land and A. G. Doig.10

This algorithm is quite similar in structure to the BIP algorithm presented in the pre- ceding section. Solving LP relaxations again provides the basis for both the bounding and fathoming steps. In fact, only four changes are needed in the BIP algorithm to deal with the generalizations from binary to general integer variables and from pure IP to mixed IP.

One change involves the choice of the branching variable. Before, the next variable in the natural ordering—x1, x2, . . . , xn—was chosen automatically. Now, the only vari- ables considered are the integer-restricted variables that have a noninteger value in the optimal solution for the LP relaxation of the current subproblem. Our rule for choosing among these variables is to select the first one in the natural ordering. (Production codes generally use a more sophisticated rule.)

The second change involves the values assigned to the branching variable for creat- ing the new smaller subproblems. Before, the binary variable was fixed at 0 and 1, re- spectively, for the two new subproblems. Now, the general integer-restricted variable could have a very large number of possible integer values, and it would be inefficient to create and analyze many subproblems by fixing the variable at its individual integer values. Therefore, what is done instead is to create just two new subproblems (as before) by spec- ifying two ranges of values for the variable.

To spell out how this is done, let xj be the current branching variable, and let xj* be

its (noninteger) value in the optimal solution for the LP relaxation of the current subproblem. Using square brackets to denote [xj*] = greatest integer < xj*,

9R. J. Dakin, “A Tree Search Algorithm for Mixed Integer Programming Problems,” Computer Journal, 8(3): 250–255, 1965.

10A. H. Land and A. G. Doig, “An Automatic Method of Solving Discrete Programming Problems,” Econo- metrica, 28: 497–520, 1960.

When the two changes to the BIP algorithm described above are combined, an inter- esting phenomenon of a recurring branching variable can occur. To illustrate, as shown in Fig. 12.10, let j = 1 in the above example where x = 31, and consider the new subprob- lem where x1 < 3. When the LP relaxation of a descendant of this subproblem is solved,

1

suppose that x1* = 1--. Then x

recurs as the branching variable, and the two new subproblems created have the additional constraint x1 < 1 and x1 ::: 2, respectively (as well as the previous additional constraint x1 < 3). Later, when the LP relaxation for a descendant of, say, the x1 < 1 subproblem is solved, suppose that x1* = --. Then x recurs again as the branching variable, and the two new subproblems created have x1 = 0 (because of the new x1 < 0 constraint and the nonnegativity constraint on x1) and x1 = 1 (because of the new x1 ::: 1 constraint and the previous x1 < 1 constraint).

The third change involves the bounding step. Before, with a pure IP problem and integer coefficients in the objective function, the value of Z for the optimal solution for the subproblem’s LP relaxation was rounded down to obtain the bound, because any feasible solution for the subproblem must have an integer Z. Now, with some of the variables not integer-restricted, the bound is the value of Z without rounding down.

The fourth (and final) change to the BIP algorithm to obtain our MIP algorithm involves fathoming test 3. Before, with a pure IP problem, the test was that the optimal so- lution for the subproblem’s LP relaxation is integer, since this ensures that the solution is feasible, and therefore optimal, for the subproblem. Now, with a mixed IP problem, the test requires only that the integer-restricted variables be integer in the optimal solution for the subproblem’s LP relaxation, because this suffices to ensure that the solution is feasible, and therefore optimal, for the subproblem.

Incorporating these four changes into the summary presented in the preceding sec- tion for the BIP algorithm yields the following summary for the new algorithm for MIP.

An Application Vignette

With headquarters in Houston, Texas, Waste Management, Inc. (a Fortune 100 company) is the leading provider of comprehensive waste-management services and integrated environmental solutions in North America. With 21,000 collection and transfer vehicles, its 45,000 employees provide services to over 20 million customers throughout the United States and Canada.

The company’s collection-and-transfer vehicles need to follow nearly 20,000 daily routes. With an annual operating cost of nearly $120,000 per vehicle, management wanted to have a comprehensive route-management system that would make every route as profitable and efficient as possible. Therefore, an OR team that included a number of consultants was formed to attack this problem.

The heart of the route-management system developed by this team is a huge mixed BIP model that optimizes the routes assigned to the respective collection- and-transfer vehicles. Although the objective function takes several factors into account, the primary goal is the minimization of total travel time. The main decision variables are binary variables that equal 1 if the route assigned to a particular vehicle includes a particular possible leg and equal 0 otherwise. A geographical information system (GIS) provides the data about the distance and time required to go between any two points. All of this is imbedded within a Web-based Java application that is integrated with the company’s other systems.

Soon after the implementation of this comprehensive route-management system, it was estimated that the system will increase the company’s cash flow by

$648 million over a 5-year period, largely because of savings of $498 million in operational expenses over this same period. It also is providing better customer service.

Source: S. Sahoo, S. Kim, B.-I. Kim, B. Krass, and A. Popov, Jr.: “Routing Optimization for Waste Management,” Interfaces, 35(1): 24–36, Jan.–Feb. 2005. (A link to this article is provided on our website, www.mhhe.com/hillier.)

(As before, this summary assumes that the objective function is to be maximized, but the only change needed for minimization is to change the direction of the inequality for fathoming test 1.)

Summary of the MIP Branch-and-Bound Algorithm

Initialization: Set Z* = -oo. Apply the bounding step, fathoming step, and optimality test described below to the whole problem. If not fathomed, classify this problem as the one remaining subproblem for performing the first full iteration below.

Steps for each iteration:

1. Branching: Among the remaining (unfathomed) subproblems, select the one that was created most recently. (Break ties according to which has the larger bound.) Among the integer-restricted variables that have a noninteger value in the optimal solution for the LP relaxation of the subproblem, choose the first one in the natural ordering of the variables to be the branching variable. Let xj be this variable and xj* its value in this solution. Branch from the node for the subproblem to create two new subproblems by adding the respective constraints xj < [xj*] and xj ::: [xj*] + 1.

2. Bounding: For each new subproblem, obtain its bound by applying the simplex method (or the dual simplex method when reoptimizing) to its LP relaxation and using the value of Z for the resulting optimal solution.

3. Fathoming: For each new subproblem, apply the three fathoming tests given below, and discard those subproblems that are fathomed by any of the tests.

Test 1: Its bound < Z*, where Z* is the value of Z for the current incumbent.

Test 2: Its LP relaxation has no feasible solutions.

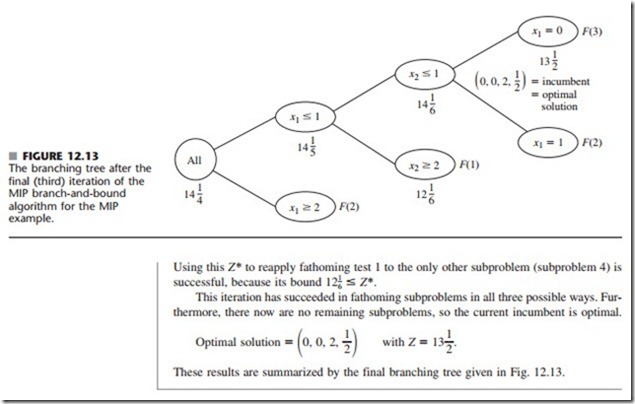
Test 3: The optimal solution for its LP relaxation has integer values for the integer- restricted variables. (If this solution is better than the incumbent, it becomes the new incumbent and test 1 is reapplied to all unfathomed subproblems with the new larger Z*.)

Optimality test: Stop when there are no remaining subproblems that are not fathomed; the current incumbent is optimal.11 Otherwise, perform another iteration.

Another example of applying the MIP algorithm is presented in your OR Tutor. In addition, a small example (only two variables, both integer-restricted) that includes graphical displays is provided in the Solved Examples section of the book’s website. The IOR Tutorial also includes an interactive procedure for executing the MIP algorithm.