Example with a Dummy Destination
Example with a Dummy Destination
The NORTHERN AIRPLANE COMPANY builds commercial airplanes for various airline companies around the world. The last stage in the production process is to produce the jet engines and then to install them (a very fast operation) in the completed airplane frame. The company has been working under some contracts to deliver a considerable number of airplanes in the near future, and the production of the jet engines for these planes must now be scheduled for the next four months.
To meet the contracted dates for delivery, the company must supply engines for installation in the quantities indicated in the second column of Table 9.7. Thus, the cumu- lative number of engines produced by the end of months 1, 2, 3, and 4 must be at least 10, 25, 50, and 70, respectively.
The facilities that will be available for producing the engines vary according to other production, maintenance, and renovation work scheduled during this period. The result- ing monthly differences in the maximum number that can be produced and the cost (in millions of dollars) of producing each one are given in the third and fourth columns of Table 9.7.
Because of the variations in production costs, it may well be worthwhile to produce some of the engines a month or more before they are scheduled for installation, and this possibility is being considered. The drawback is that such engines must be stored until the scheduled installation (the airplane frames will not be ready early) at a storage cost of $15,000 per month (including interest on expended capital) for each engine,1 as shown in the rightmost column of Table 9.7.
The production manager wants a schedule developed for the number of engines to be produced in each of the four months so that the total of the production and storage costs will be minimized.
Formulation. One way to formulate a mathematical model for this problem is to let xj
be the number of jet engines to be produced in month j, for j = 1, 2, 3, 4. By using only
1For modeling purposes, assume that this storage cost is incurred at the end of the month for just those engines that are being held over into the next month. Thus, engines that are produced in a given month for installation in the same month are assumed to incur no storage cost.
these four decision variables, the problem can be formulated as a linear programming problem that does not fit the transportation problem type. (See Prob. 9.2-18.)
On the other hand, by adopting a different viewpoint, we can instead formulate the problem as a transportation problem that requires much less effort to solve. This view- point will describe the problem in terms of sources and destinations and then identify the corresponding xij, cij, si, and dj. (See if you can do this before reading further.)
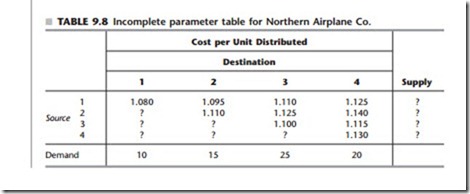
Because the units being distributed are jet engines, each of which is to be scheduled for production in a particular month and then installed in a particular (perhaps different) month,

Since it is impossible to produce engines in one month for installation in an earlier month, xij must be zero if i > j. Therefore, there is no real cost that can be associated with such xij. Nevertheless, in order to have a well-defined transportation problem to which the solution procedure of Sec. 9.2 can be applied, it is necessary to assign some value for the unidentified costs. Fortunately, we can use the Big M method introduced in Sec. 4.6 to
assign this value. Thus, we assign a very large number (denoted by M for convenience) to the unidentified cost entries in Table 9.8 to force the corresponding values of xij to be zero in the final solution.
The numbers that need to be inserted into the supply column of Table 9.8 are not obvious because the “supplies,” the amounts produced in the respective months, are not fixed quantities. In fact, the objective is to solve for the most desirable values of these production quantities. Nevertheless, it is necessary to assign some fixed number to every entry in the table, including those in the supply column, to have a transportation problem. A clue is pro- vided by the fact that although the supply constraints are not present in the usual form, these constraints do exist in the form of upper bounds on the amount that can be supplied, namely,
The only change from the standard model for the transportation problem is that these con- straints are in the form of inequalities instead of equalities.
To convert these inequalities to equations in order to fit the transportation problem model, we use the familiar device of slack variables, introduced in Sec. 4.2. In this con- text, the slack variables are allocations to a single dummy destination that represent the unused production capacity in the respective months. This change permits the supply in the transportation problem formulation to be the total production capacity in the given month. Furthermore, because the demand for the dummy destination is the total unused capacity, this demand is
(25 + 35 + 30 + 10) - (10 + 15 + 25 + 20) = 30.
With this demand included, the sum of the supplies now equals the sum of the demands, which is the condition given by the feasible solutions property for having feasible solutions.
The cost entries associated with the dummy destination should be zero because there is no cost incurred by a fictional allocation. (Cost entries of M would be inappropriate for this column because we do not want to force the corresponding values of xij to be zero. In fact, these values need to sum to 30.)
The resulting final parameter table is given in Table 9.9, with the dummy destination labeled as destination 5(D). By using this formulation, it is quite easy to find the optimal production schedule by the solution procedure described in Sec. 9.2. (See Prob. 9.2-10 and its answer in the back of the book.)






Comments
Post a Comment