THE TRANSPORTATION AND ASSIGNMENT PROBLEMS:A STREAMLINED SIMPLEX METHOD FOR THE TRANSPORTATION PROBLEM

A STREAMLINED SIMPLEX METHOD FOR THE TRANSPORTATION PROBLEM

Because the transportation problem is just a special type of linear programming problem, it can be solved by applying the simplex method as described in Chap. 4. However, you will see in this section that some tremendous computational shortcuts can be taken in this method by exploiting the special structure shown in Table 9.6. We shall refer to this stream- lined procedure as the transportation simplex method.

As you read on, note particularly how the special structure is exploited to achieve great computational savings. This will illustrate an important OR technique—streamlining an algorithm to exploit the special structure in the problem at hand.

Setting Up the Transportation Simplex Method

To highlight the streamlining achieved by the transportation simplex method, let us first review how the general (unstreamlined) simplex method would set up a transportation prob- lem in tabular form. After constructing the table of constraint coefficients (see Table 9.6), converting the objective function to maximization form, and using the Big M method to introduce artificial variables z1, z2, . . . , zm+n into the m + n respective equality con- straints (see Sec. 4.6), typical columns of the simplex tableau would have the form shown in Table 9.13, where all entries not shown in these columns are zeros. [The one remaining adjustment to be made before the first iteration of the simplex method is to algebraically eliminate the nonzero coefficients of the initial (artificial) basic variables in row 0.]

After any subsequent iteration, row 0 then would have the form shown in Table 9.14. Because of the pattern of 0s and 1s for the coefficients in Table 9.13, by the fundamen- tal insight presented in Sec. 5.3, ui and vj would have the following interpretation:

ui = multiple of original row i that has been subtracted (directly or indirectly) from original row 0 by the simplex method during all iterations leading to the cur- rent simplex tableau.

vj = multiple of original row m + j that has been subtracted (directly or indirectly) from original row 0 by the simplex method during all iterations leading to the current simplex tableau.

The Needed Information. To lay the groundwork for simplifying this setup, recall what information is needed by the simplex method. In the initialization, an initial BF so- lution must be obtained, which is done artificially by introducing artificial variables as the initial basic variables and setting them equal to si and dj. The optimality test and step 1 of an iteration (selecting an entering basic variable) require knowing the current row 0, which is obtained by subtracting a certain multiple of another row from the preceding row 0. Step 2 (determining the leaving basic variable) must identify the basic variable that reaches zero first as the entering basic variable is increased, which is done by comparing the current coefficients of the entering basic variable and the corresponding right side. Step 3 must determine the new BF solution, which is found by subtracting certain multi- ples of one row from the other rows in the current simplex tableau.

Greatly Streamlined Ways of Obtaining This Information. Now, how does the transportation simplex method obtain the same information in much simpler ways? This story will unfold fully in the coming pages, but here are some preliminary answers.

First, no artificial variables are needed, because a simple and convenient procedure (with several variations) is available for constructing an initial BF solution.

Second, the current row 0 can be obtained without using any other row simply by cal- culating the current values of ui and vj directly. Since each basic variable must have a co- efficient of zero in row 0, the current ui and vj are obtained by solving the set of equations

cij - ui - vj = 0 for each i and j such that xij is a basic variable.

(We will illustrate this straightforward procedure later when discussing the optimality test for the transportation simplex method.) The special structure in Table 9.13 makes this convenient way of obtaining row 0 possible by yielding cij - ui - vj as the coefficient of xij in Table 9.14.

Third, the leaving basic variable can be identified in a simple way without (explicitly)

using the coefficients of the entering basic variable. The reason is that the special structure of the problem makes it easy to see how the solution must change as the entering basic variable is increased. As a result, the new BF solution also can be identified immediately without any algebraic manipulations on the rows of the simplex tableau. (You will see the details when we describe how the transportation simplex method performs an iteration.) The grand conclusion is that almost the entire simplex tableau (and the work of main- taining it) can be eliminated! Besides the input data (the cij, si, and dj values), the only

3It would be easier to recognize these variables as dual variables by relabeling all these variables as yi and then changing all the signs in row 0 of Table 9.14 by converting the objective function back to its original mini- mization form.

information needed by the transportation simplex method is the current BF solution,4 the current values of ui and vj, and the resulting values of cij - ui - vj for nonbasic variables xij. When you solve a problem by hand, it is convenient to record this information for each iteration in a transportation simplex tableau, such as shown in Table 9.15. (Note carefully that the values of xij and cij - ui - vj are distinguished in these tableaux by cir- cling the former but not the latter.)

The Resulting Great Improvement in Efficiency. You can gain a fuller appreciation for the great difference in efficiency and convenience between the simplex and the trans- portation simplex methods by applying both to the same small problem (see Prob. 9.2-17). However, the difference becomes even more pronounced for large problems that must be solved on a computer. This pronounced difference is suggested somewhat by comparing the sizes of the simplex and the transportation simplex tableaux. Thus, for a transportation problem having m sources and n destinations, the simplex tableau would have m + n + 1 rows and (m + 1)(n + 1) columns (excluding those to the left of the xij columns), and the transportation simplex tableau would have m rows and n columns (excluding the two ex- tra informational rows and columns). Now try plugging in various values for m and n (for example, m = 10 and n = 100 would be a rather typical medium-size transportation problem), and note how the ratio of the number of cells in the simplex tableau to the number in the transportation simplex tableau increases as m and n increase.

Initialization

Recall that the objective of the initialization is to obtain an initial BF solution. Because all the functional constraints in the transportation problem are equality constraints, the simplex method would obtain this solution by introducing artificial variables and using them as the initial basic variables, as described in Sec. 4.6. The resulting basic solution

actually is feasible only for a revised version of the problem, so a number of iterations are needed to drive these artificial variables to zero in order to reach the real BF solu- tions. The transportation simplex method bypasses all this by instead using a simpler pro- cedure to directly construct a real BF solution on a transportation simplex tableau.

Before outlining this procedure, we need to point out that the number of basic vari- ables in any basic solution of a transportation problem is one fewer than you might ex- pect. Ordinarily, there is one basic variable for each functional constraint in a linear programming problem. For transportation problems with m sources and n destinations, the number of functional constraints is m + n. However,

Number of basic variables = m + n - 1.

The reason is that the functional constraints are equality constraints, and this set of m + n equations has one extra (or redundant) equation that can be deleted without chang- ing the feasible region; i.e., any one of the constraints is automatically satisfied whenever the other m + n - 1 constraints are satisfied. (This fact can be verified by showing that any supply constraint exactly equals the sum of the demand constraints minus the sum of the other supply constraints, and that any demand equation also can be reproduced by sum- ming the supply equations and subtracting the other demand equations. See Prob. 9.2-19.) Therefore, any BF solution appears on a transportation simplex tableau with exactly m + n - 1 circled nonnegative allocations, where the sum of the allocations for each row or column equals its supply or demand.5

The procedure for constructing an initial BF solution selects the m + n - 1 basic vari- ables one at a time. After each selection, a value that will satisfy one additional constraint (thereby eliminating that constraint’s row or column from further consideration for pro- viding allocations) is assigned to that variable. Thus, after m + n - 1 selections, an en- tire basic solution has been constructed in such a way as to satisfy all the constraints. A number of different criteria have been proposed for selecting the basic variables. We pre- sent and illustrate three of these criteria here, after outlining the general procedure.

General Procedure6 for Constructing an Initial BF Solution. To begin, all source rows and destination columns of the transportation simplex tableau are initially under con- sideration for providing a basic variable (allocation).

1. From the rows and columns still under consideration, select the next basic variable (al- location) according to some criterion.

2. Make that allocation large enough to exactly use up the remaining supply in its row or the remaining demand in its column (whichever is smaller).

3. Eliminate that row or column (whichever had the smaller remaining supply or demand) from further consideration. (If the row and column have the same remaining supply and demand, then arbitrarily select the row as the one to be eliminated. The column will be used later to provide a degenerate basic variable, i.e., a circled allocation of zero.)

4. If only one row or only one column remains under consideration, then the procedure is completed by selecting every remaining variable (i.e., those variables that were nei- ther previously selected to be basic nor eliminated from consideration by eliminating

5However, note that any feasible solution with m + n - 1 nonzero variables is not necessarily a basic solution because it might be the weighted average of two or more degenerate BF solutions (i.e., BF solutions having some basic variables equal to zero). We need not be concerned about mislabeling such solutions as being basic, however, because the transportation simplex method constructs only legitimate BF solutions.

6In Sec. 4.1 we pointed out that the simplex method is an example of the algorithms (systematic solution pro- cedures) so prevalent in OR work. Note that this procedure also is an algorithm, where each successive execu- tion of the (four) steps constitutes an iteration.

their row or column) associated with that row or column to be basic with the only feasible allocation. Otherwise, return to step 1.

Alternative Criteria for Step 1

1. Northwest corner rule: Begin by selecting x11 (that is, start in the northwest corner of the transportation simplex tableau). Thereafter, if xij was the last basic variable selected, then next select xi,j+1 (that is, move one column to the right) if source i has any sup- ply remaining. Otherwise, next select xi+1,j (that is, move one row down).

Example. To make this description more concrete, we now illustrate the general pro- cedure on the Metro Water District problem (see Table 9.12) with the northwest corner rule being used in step 1. Because m = 4 and n = 5 in this case, the procedure would find an initial BF solution having m + n - 1 = 8 basic variables.

As shown in Table 9.16, the first allocation is x11 = 30, which exactly uses up the demand in column 1 (and eliminates this column from further consideration). This first iteration leaves a supply of 20 remaining in row 1, so next select x1,1+1 = x12 to be a ba- sic variable. Because this supply is no larger than the demand of 20 in column 2, all of it is allocated, x12 = 20, and this row is eliminated from further consideration. (Row 1 is chosen for elimination rather than column 2 because of the parenthetical instruction in step 3.) Therefore, select x1+1,2 = x22 next. Because the remaining demand of 0 in col- umn 2 is less than the supply of 60 in row 2, allocate x22 = 0 and eliminate column 2.

Continuing in this manner, we eventually obtain the entire initial BF solution

shown in Table 9.16, where the circled numbers are the values of the basic variables (x11 = 30, . . . , x45 = 50) and all the other variables (x13, etc.) are nonbasic variables equal to zero. Arrows have been added to show the order in which the basic variables (al- locations) were selected. The value of Z for this solution is

Z = 16(30) + 16(20) + . . . + 0(50) = 2,470 + 10M.

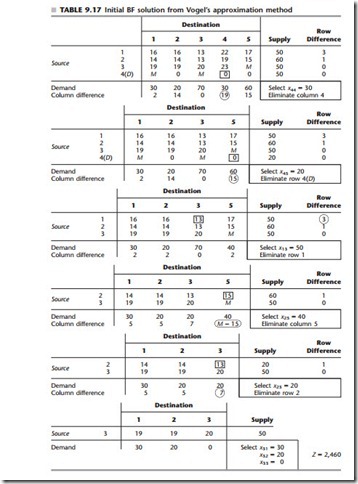
2. Vogel’s approximation method: For each row and column remaining under consider- ation, calculate its difference, which is defined as the arithmetic difference between the smallest and next-to-the-smallest unit cost cij still remaining in that row or col- umn. (If two unit costs tie for being the smallest remaining in a row or column, then

Example. Now let us apply the general procedure to the Metro Water District problem by using the criterion for Vogel’s approximation method to select the next basic variable in step 1. With this criterion, it is more convenient to work with parameter tables (rather than with complete transportation simplex tableaux), beginning with the one shown in Table 9.12. At each iteration, after the difference for every row and column remaining un- der consideration is calculated and displayed, the largest difference is circled and the small- est unit cost in its row or column is enclosed in a box. The resulting selection (and value) of the variable having this unit cost as the next basic variable is indicated in the lower right-hand corner of the current table, along with the row or column thereby being elim- inated from further consideration (see steps 2 and 3 of the general procedure). The table for the next iteration is exactly the same except for deleting this row or column and sub- tracting the last allocation from its supply or demand (whichever remains).

Applying this procedure to the Metro Water District problem yields the sequence of parameter tables shown in Table 9.17, where the resulting initial BF solution consists of the eight basic variables (allocations) given in the lower right-hand corner of the respective parameter tables.

This example illustrates two relatively subtle features of the general procedure that war- rant special attention. First, note that the final iteration selects three variables (x31, x32, and x33) to become basic instead of the single selection made at the other iterations. The reason is that only one row (row 3) remains under consideration at this point. Therefore, step 4 of the general procedure says to select every remaining variable associated with row 3 to be basic.

Second, note that the allocation of x23 = 20 at the next-to-last iteration exhausts both the remaining supply in its row and the remaining demand in its column. However, rather than eliminate both the row and column from further consideration, step 3 says to eliminate only the row, saving the column to provide a degenerate basic variable later. Column 3 is, in fact, used for just this purpose at the final iteration when x33 = 0 is selected as one of the basic variables. For another illustration of this same phenomenon, see Table 9.16 where the allocation of x12 = 20 results in eliminating only row 1, so that column 2 is saved to provide a degenerate basic variable, x22 = 0, at the next iteration.

Although a zero allocation might seem irrelevant, it actually plays an important role.

You will see soon that the transportation simplex method must know all m + n - 1 basic variables, including those with value zero, in the current BF solution.

3. Russell’s approximation method: For each source row i remaining under consideration, determine its ui, which is the largest unit cost cij still remaining in that row. For each destination column j remaining under consideration, determine its v j, which is the largest unit cost cij still remaining in that column. For each variable xij not previously selected in these rows and columns, calculate llij = cij - ui - vj. Select the variable having the largest (in absolute terms) negative value of llij. (Ties may be broken arbitrarily.)

Example. Using the criterion for Russell’s approximation method in step 1, we again apply the general procedure to the Metro Water District problem (see Table 9.12). The re- sults, including the sequence of basic variables (allocations), are shown in Table 9.18.

Calculating all the llij values for i = 1, 2, 3, 4 and j = 1, 2, 3, 4, 5 shows that ll45 = 0 - 2M has the largest negative value, so x45 = 50 is selected as the first basic variable (allocation). This allocation exactly uses up the supply in row 4, so this row is eliminated from further consideration.

Note that eliminating this row changes v 1 and v 3 for the next iteration. Therefore, the second iteration requires recalculating the llij with j = 1, 3 as well as eliminating i = 4.

The largest negative value now is

ll15 = 17 - 22 - M = -5 - M,

so x15 = 10 becomes the second basic variable (allocation), eliminating column 5 from further consideration.

The subsequent iterations proceed similarly, but you may want to test your under- standing by verifying the remaining allocations given in Table 9.18. As with the other pro- cedures in this (and other) section(s), you should find your IOR Tutorial useful for doing the calculations involved and illuminating the approach. (See the interactive procedure for finding an initial BF solution.)

Comparison of Alternative Criteria for Step 1. Now let us compare these three criteria for selecting the next basic variable. The main virtue of the northwest corner rule is that it is quick and easy. However, because it pays no attention to unit costs cij, usually the solution obtained will be far from optimal. (Note in Table 9.16 that x35 = 10 even though c35 = M.) Expending a little more effort to find a good initial BF solution might greatly reduce the number of iterations then required by the transportation simplex method to reach an optimal solution (see Probs. 9.2-7 and 9.2-9). Finding such a solution is the objective of the other two criteria.

Vogel’s approximation method has been a popular criterion for many years,7 partially because it is relatively easy to implement by hand. Because the difference represents the minimum extra unit cost incurred by failing to make an allocation to the cell having the smallest unit cost in that row or column, this criterion does take costs into account in an effective way.

Russell’s approximation method provides another excellent criterion8 that is still quick to implement on a computer (but not manually). Although it is unclear as to which is more

effective on average, this criterion frequently does obtain a better solution than Vogel’s. (For the example, Vogel’s approximation method happened to find the optimal solution with Z = 2,460, whereas Russell’s misses slightly with Z = 2,570.) For a large problem, it may be worthwhile to apply both criteria and then use the better solution to start the it- erations of the transportation simplex method.

One distinct advantage of Russell’s approximation method is that it is patterned di- rectly after step 1 for the transportation simplex method (as you will see soon), which somewhat simplifies the overall computer code. In particular, the u i and vj values have been defined in such a way that the relative values of the cij - ui - vj estimate the rela- tive values of cij - ui - vj that will be obtained when the transportation simplex method reaches an optimal solution.

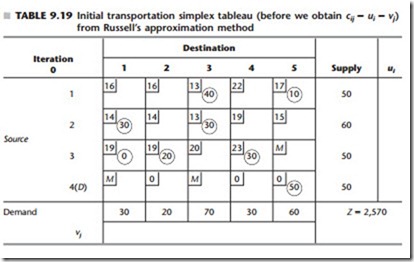
We now shall use the initial BF solution obtained in Table 9.18 by Russell’s approxi- mation method to illustrate the remainder of the transportation simplex method. Thus, our initial transportation simplex tableau (before we solve for ui and vj) is shown in Table 9.19.

The next step is to check whether this initial solution is optimal by applying the op-

timality test.

Optimality Test

Using the notation of Table 9.14, we can reduce the standard optimality test for the sim- plex method (see Sec. 4.3) to the following for the transportation problem:

Optimality test: A BF solution is optimal if and only if cij - ui - vj > 0 for every (i, j) such that xij is nonbasic.9

Thus, the only work required by the optimality test is the derivation of the values of ui and vj for the current BF solution and then the calculation of these cij - ui - vj, as de- scribed below.

Setting u3 = 0 (since row 3 of Table 9.19 has the largest number of allocations—3) and moving down the equations one at a time immediately give the derivation of values for the unknowns shown to the right of the equations. (Note that this derivation of the ui and vj values depends on which xij variables are basic variables in the current BF solution, so this derivation will need to be repeated each time a new BF solution is obtained.)

Once you get the hang of it, you probably will find it even more convenient to solve these equations without writing them down by working directly on the transportation sim- plex tableau. Thus, in Table 9.19 you begin by writing in the value u3 = 0 and then pick- ing out the circled allocations (x31, x32, x34) in that row. For each one you set vj = c3j and then look for circled allocations (except in row 3) in these columns (x21). Mentally calculate u2 = c21 - v1, pick out x23, set v3 = c23 - u2, and so on until you have filled in all the values for ui and vj. (Try it.) Then calculate and fill in the value of cij - ui - vj for each nonbasic variable xij (that is, for each cell without a circled allocation), and you will have the completed initial transportation simplex tableau shown in Table 9.20.

We are now in a position to apply the optimality test by checking the values of cij - ui - vj given in Table 9.20. Because two of these values (c25 - u2 - v5 = -2 and c44 - u4 - v4 = -1) are negative, we conclude that the current BF solution is not opti- mal. Therefore, the transportation simplex method must next go to an iteration to find a better BF solution.

An Iteration

As with the full-fledged simplex method, an iteration for this streamlined version must determine an entering basic variable (step 1), a leaving basic variable (step 2), and then identify the resulting new BF solution (step 3).

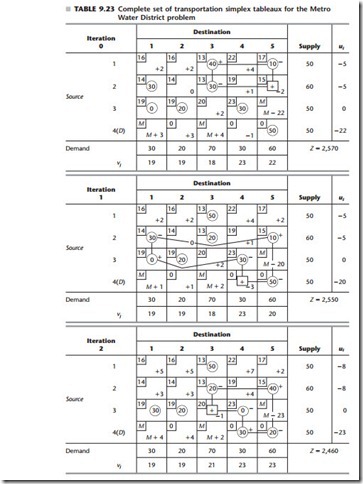
Step 1: Find the Entering Basic Variable. Since cij - ui - vj represents the rate at which the objective function will change as the nonbasic variable xij is increased, the en- tering basic variable must have a negative cij - ui - vj value to decrease the total cost Z. Thus, the candidates in Table 9.20 are x25 and x44. To choose between the candidates, se- lect the one having the larger (in absolute terms) negative value of cij - ui - vj to be the entering basic variable, which is x25 in this case.

Step 2: Find the Leaving Basic Variable. Increasing the entering basic variable from zero sets off a chain reaction of compensating changes in other basic variables (alloca- tions), in order to continue satisfying the supply and demand constraints. The first basic variable to be decreased to zero then becomes the leaving basic variable.

With x25 as the entering basic variable, the chain reaction in Table 9.20 is the rela- tively simple one summarized in Table 9.21. (We shall always indicate the entering basic variable by placing a boxed plus sign in the center of its cell while leaving the corre- sponding value of cij - ui - vj in the lower right-hand corner of this cell.) Increasing x25 by some amount requires decreasing x15 by the same amount to restore the demand of 60 in column 5. This change then requires increasing x13 by this same amount to restore the

supply of 50 in row 1. This change then requires decreasing x23 by this amount to re- store the demand of 70 in column 3. This decrease in x23 successfully completes the chain reaction because it also restores the supply of 60 in row 2. (Equivalently, we could have started the chain reaction by restoring this supply in row 2 with the de- crease in x23, and then the chain reaction would continue with the increase in x13 and decrease in x15.)

The net result is that cells (2, 5) and (1, 3) become recipient cells, each receiving its additional allocation from one of the donor cells, (1, 5) and (2, 3). (These cells are indi- cated in Table 9.21 by the plus and minus signs.) Note that cell (1, 5) had to be the donor cell for column 5 rather than cell (4, 5), because cell (4, 5) would have no recipient cell in row 4 to continue the chain reaction. [Similarly, if the chain reaction had been started in row 2 instead, cell (2, 1) could not be the donor cell for this row because the chain re- action could not then be completed successfully after necessarily choosing cell (3, 1) as the next recipient cell and either cell (3, 2) or (3, 4) as its donor cell.] Also note that, ex- cept for the entering basic variable, all recipient cells and donor cells in the chain reaction must correspond to basic variables in the current BF solution.

Each donor cell decreases its allocation by exactly the same amount as the entering basic variable (and other recipient cells) is increased. Therefore, the donor cell that starts with the smallest allocation—cell (1, 5) in this case (since 10 < 30 in Table 9.21)—must reach a zero allocation first as the entering basic variable x25 is increased. Thus, x15 be- comes the leaving basic variable.

In general, there always is just one chain reaction (in either direction) that can be completed successfully to maintain feasibility when the entering basic variable is increased from zero. This chain reaction can be identified by selecting from the cells having a ba- sic variable: first the donor cell in the column having the entering basic variable, then the recipient cell in the row having this donor cell, then the donor cell in the column having this recipient cell, and so on until the chain reaction yields a donor cell in the row hav- ing the entering basic variable. When a column or row has more than one additional ba- sic variable cell, it may be necessary to trace them all further to see which one must be selected to be the donor or recipient cell. (All but this one eventually will reach a dead end in a row or column having no additional basic variable cell.) After the chain reaction is identified, the donor cell having the smallest allocation automatically provides the leav- ing basic variable. (In the case of a tie for the donor cell having the smallest allocation, any one can be chosen arbitrarily to provide the leaving basic variable.)

Step 3: Find the New BF Solution. The new BF solution is identified simply by adding the value of the leaving basic variable (before any change) to the allocation for each recipient cell and subtracting this same amount from the allocation for each donor cell. In Table 9.21 the value of the leaving basic variable x15 is 10, so the portion of the transportation simplex tableau in this table changes as shown in Table 9.22 for the new solution. (Since x15 is non- basic in the new solution, its new allocation of zero is no longer shown in this new tableau.) We can now highlight a useful interpretation of the cij - ui - vj quantities derived during the optimality test. Because of the shift of 10 allocation units from the donor cellsto the recipient cells (shown in Tables 9.21 and 9.22), the total cost changes by

llZ = 10(15 - 17 + 13 - 13) = 10(-2) = 10(c25 - u2 - v5).

Thus, the effect of increasing the entering basic variable x25 from zero has been a cost change at the rate of -2 per unit increase in x25. This is precisely what the value of c25 - u2 - v5 = -2 in Table 9.20 indicates would happen. In fact, another (but less effi- cient) way of deriving cij - ui - vj for each nonbasic variable xij is to identify the chain reaction caused by increasing this variable from 0 to 1 and then to calculate the resulting

Iteration:

1. Determine the entering basic variable: Select the nonbasic variable xij having the largest

(in absolute terms) negative value of cij - ui - vj.

2. Determine the leaving basic variable: Identify the chain reaction required to retain fea-

sibility when the entering basic variable is increased. From the donor cells, select the basic variable having the smallest value.

3. Determine the new BF solution: Add the value of the leaving basic variable to the allo- cation for each recipient cell. Subtract this value from the allocation for each donor cell.

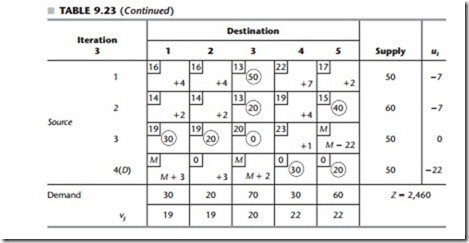
Continuing to apply this procedure to the Metro Water District problem yields the complete set of transportation simplex tableaux shown in Table 9.23. Since all the cij - ui - vj values are nonnegative in the fourth tableau, the optimality test identifies the set of allocations in this tableau as being optimal, which concludes the algorithm.

It would be good practice for you to derive the values of ui and vj given in the second, third, and fourth tableaux. Try doing this by working directly on the tableaux. Also check out the chain reactions in the second and third tableaux, which are somewhat more complicated than the one you have seen in Table 9.21.

Special Features of This Example

Note three special points that are illustrated by this example. First, the initial BF solution is degenerate because the basic variable x31 = 0. However, this degenerate basic variable causes no complication, because cell (3, 1) becomes a recipient cell in the second tableau, which increases x31 to a value greater than zero.

Second, another degenerate basic variable (x34) arises in the third tableau because the basic variables for two donor cells in the second tableau, cells (2, 1) and (3, 4), tie for having the smallest value (30). (This tie is broken arbitrarily by selecting x21 as the leaving basic variable; if x34 had been selected instead, then x21 would have be- come the degenerate basic variable.) This degenerate basic variable does appear to cre- ate a complication subsequently, because cell (3, 4) becomes a donor cell in the third tableau but has nothing to donate! Fortunately, such an event actually gives no cause for concern. Since zero is the amount to be added to or subtracted from the alloca- tions for the recipient and donor cells, these allocations do not change. However, the degenerate basic variable does become the leaving basic variable, so it is replaced by the entering basic variable as the circled allocation of zero in the fourth tableau. This change in the set of basic variables changes the values of ui and vj. Therefore, if any of the cij - ui - vj had been negative in the fourth tableau, the algorithm would have gone on to make real changes in the allocations (whenever all donor cells have non- degenerate basic variables).

Third, because none of the cij - ui - vj turned out to be negative in the fourth tableau, the equivalent set of allocations in the third tableau is optimal also. Thus, the algorithm executed one more iteration than was necessary. This extra iteration is a flaw that occa- sionally arises in both the transportation simplex method and the simplex method be- cause of degeneracy, but it is not sufficiently serious to warrant any adjustments to these algorithms.

If you would like to see additional (smaller) examples of the application of the trans- portation simplex method, two are available. One is the demonstration provided for the transportation problem area in your OR Tutor. In addition, the Solved Examples section of the book’s website includes another example of this type. Also provided in your IOR Tutorial are both an interactive procedure and an automatic procedure for the transportation simplex method.

Now that you have studied the transportation simplex method, you are in a position to check for yourself how the algorithm actually provides a proof of the integer so- lutions property presented in Sec. 9.1. Problem 9.2-20 helps to guide you through the reasoning.