INTRODUCTION TO LINEAR PROGRAMMING:THE LINEAR PROGRAMMING MODEL

 THE LINEAR PROGRAMMING MODEL

The Wyndor Glass Co. problem is intended to illustrate a typical linear programming problem (miniature version). However, linear programming is too versatile to be completely characterized by a single example. In this section we discuss the general characteristics of linear programming problems, including the various legitimate forms of the mathematical model for linear programming.

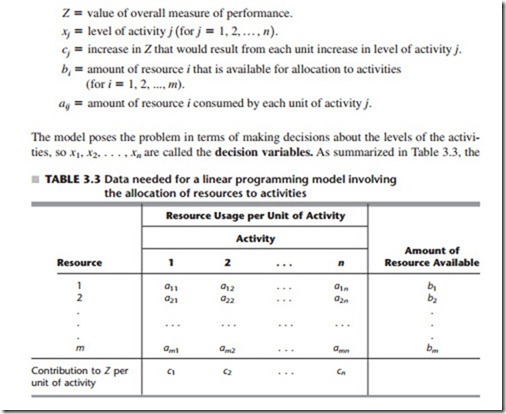
Let us begin with some basic terminology and notation. The first column of Table 3.2 summarizes the components of the Wyndor Glass Co. problem. The second column then introduces more general terms for these same components that will fit many linear pro- gramming problems. The key terms are resources and activities, where m denotes the num- ber of different kinds of resources that can be used and n denotes the number of activities being considered. Some typical resources are money and particular kinds of machines,

equipment, vehicles, and personnel. Examples of activities include investing in particular projects, advertising in particular media, and shipping goods from a particular source to a particular destination. In any application of linear programming, all the activities may be of one general kind (such as any one of these three examples), and then the individual activities would be particular alternatives within this general category.

As described in the introduction to this chapter, the most common type of application of linear programming involves allocating resources to activities. The amount available of each resource is limited, so a careful allocation of resources to activities must be made. Determining this allocation involves choosing the levels of the activities that achieve the best possible value of the overall measure of performance.

Certain symbols are commonly used to denote the various components of a linear pro- gramming model. These symbols are listed below, along with their interpretation for the general problem of allocating resources to activities.

A Standard Form of the Model

Proceeding as for the Wyndor Glass Co. problem, we can now formulate the mathematical model for this general problem of allocating resources to activities. In particular, this model is to select the values for x1, x2, . . . , xn so as to

Any problem that mixes some or all of these forms with the remaining parts of the preced- ing model is still a linear programming problem. Our interpretation of the words allocating

1This is called our standard form rather than the standard form because some textbooks adopt other forms.

limited resources among competing activities may no longer apply very well, if at all; but regardless of the interpretation or context, all that is required is that the mathematical state- ment of the problem fit the allowable forms. Thus, the concise definition of a linear pro- gramming problem is that each component of its model fits either the standard form or one of the other legitimate forms listed above.

Terminology for Solutions of the Model

You may be used to having the term solution mean the final answer to a problem, but the convention in linear programming (and its extensions) is quite different. Here, any specifi- cation of values for the decision variables (x1, x2,... , xn) is called a solution, regardless of whether it is a desirable or even an allowable choice. Different types of solutions are then identified by using an appropriate adjective.

A feasible solution is a solution for which all the constraints are satisfied.

An infeasible solution is a solution for which at least one constraint is violated.

In the example, the points (2, 3) and (4, 1) in Fig. 3.2 are feasible solutions, while the points ( -1, 3) and (4, 4) are infeasible solutions.

The feasible region is the collection of all feasible solutions.

The feasible region in the example is the entire shaded area in Fig. 3.2.

It is possible for a problem to have no feasible solutions. This would have happened in the example if the new products had been required to return a net profit of at least

$50,000 per week to justify discontinuing part of the current product line. The correspond- ing constraint, 3x1 + 5x2 ::: 50, would eliminate the entire feasible region, so no mix of new products would be superior to the status quo. This case is illustrated in Fig. 3.4.

Given that there are feasible solutions, the goal of linear programming is to find a best feasible solution, as measured by the value of the objective function in the model.

An optimal solution is a feasible solution that has the most favorable value of the objective function.

The most favorable value is the largest value if the objective function is to be maximized,

whereas it is the smallest value if the objective function is to be minimized.

Most problems will have just one optimal solution. However, it is possible to have more than one. This would occur in the example if the profit per batch produced of product 2 were changed to $2,000. This changes the objective function to Z = 3x1 + 2x2, so that all the points on the line segment connecting (2, 6) and (4, 3) would be optimal. This case is illustrated in Fig. 3.5. As in this case, any problem having multiple optimal solutions will have an infinite number of them, each with the same optimal value of the objective function.

Another possibility is that a problem has no optimal solutions. This occurs only if (1) it has no feasible solutions or (2) the constraints do not prevent improving the value of the objective function (Z) indefinitely in the favorable direction (positive or negative). The latter case is referred to as having an unbounded Z or an unbounded objective. To illustrate, this case would result if the last two functional constraints were mistakenly deleted in the example, as illustrated in Fig. 3.6.

We next introduce a special type of feasible solution that plays the key role when the simplex method searches for an optimal solution.

A corner-point feasible (CPF) solution is a solution that lies at a corner of the feasible region.

(CPF solutions are commonly referred to as extreme points (or vertices) by OR professionals, but we prefer the more suggestive corner-point terminology in an introductory course.) Figure 3.7 highlights the five CPF solutions for the example.

Sections 4.1 and 5.1 will delve into the various useful properties of CPF solutions for problems of any size, including the following relationship with optimal solutions.

Relationship between optimal solutions and CPF solutions: Consider any lin- ear programming problem with feasible solutions and a bounded feasible region. The problem must possess CPF solutions and at least one optimal solution. Fur- thermore, the best CPF solution must be an optimal solution. Thus, if a problem has exactly one optimal solution, it must be a CPF solution. If the problem has multiple optimal solutions, at least two must be CPF solutions.

The example has exactly one optimal solution, (x1, x2) = (2, 6), which is a CPF solution. (Think about how the graphical method leads to the one optimal solution being a CPF solution.) When the example is modified to yield multiple optimal solutions, as shown in Fig. 3.5, two of these optimal solutions—(2, 6) and (4, 3)—are CPF solutions.