INTRODUCTION TO LINEAR PROGRAMMING:ASSUMPTIONS OF LINEAR PROGRAMMING

ASSUMPTIONS OF LINEAR PROGRAMMING

All the assumptions of linear programming actually are implicit in the model formulation given in Sec. 3.2. In particular, from a mathematical viewpoint, the assumptions simply are that the model must have a linear objective function subject to linear constraints. However, from a modeling viewpoint, these mathematical properties of a linear programming model imply that certain assumptions must hold about the activities and data of the problem being modeled, including assumptions about the effect of varying the levels of the activities. It is good to highlight these assumptions so you can more easily evaluate how well linear pro- gramming applies to any given problem. Furthermore, we still need to see why the OR team for the Wyndor Glass Co. concluded that a linear programming formulation provided a satisfactory representation of the problem.

Proportionality

Proportionality is an assumption about both the objective function and the functional con- straints, as summarized below.

Proportionality assumption: The contribution of each activity to the value of the objective function Z is proportional to the level of the activity xj, as represented by the cjxj term in the objective function. Similarly, the contribution of each activity to the left-hand side of each functional constraint is proportional to the level of the activity xj, as represented by the aijxj term in the constraint. Consequently, this assumption rules out any exponent other than 1 for any variable in any term of any function (whether the objective function or the function on the left-hand side of a functional constraint) in a linear programming model.2

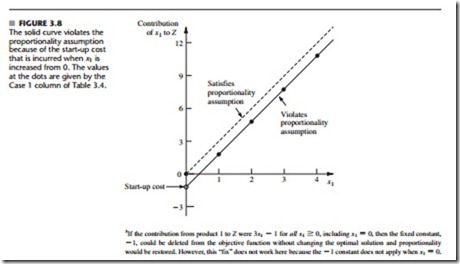
To illustrate this assumption, consider the first term (3x1) in the objective function (Z = 3x1 + 5x2) for the Wyndor Glass Co. problem. This term represents the profit gener- ated per week (in thousands of dollars) by producing product 1 at the rate of x1 batches per week. The proportionality satisfied column of Table 3.4 shows the case that was assumed in Sec. 3.1, namely, that this profit is indeed proportional to x1 so that 3x1 is the appropri- ate term for the objective function. By contrast, the next three columns show different hypothetical cases where the proportionality assumption would be violated.

Refer first to the Case 1 column in Table 3.4. This case would arise if there were start-up costs associated with initiating the production of product 1. For example, there might be costs involved with setting up the production facilities. There might also be costs associated with arranging the distribution of the new product. Because these are one-time costs, they would need to be amortized on a per-week basis to be commensurable with Z (profit in thousands of dollars per week). Suppose that this amortization were done and that the total start-up cost amounted to reducing Z by 1, but that the profit without considering the start-up cost would be 3x1. This would mean that the contribution from product 1 to Z should be 3x1 - 1 for x1 > 0,

2When the function includes any cross-product terms, proportionality should be interpreted to mean that changes in the function value are proportional to changes in each variable (xj) individually, given any fixed values for all the other variables. Therefore, a cross-product term satisfies proportionality as long as each variable in the term has an exponent of 1 (However, any cross-product term violates the additivity assumption, discussed next.)

whereas the contribution would be 3x1 = 0 when x1 = 0 (no start-up cost). This profit func- tion,3 which is given by the solid curve in Fig. 3.8, certainly is not proportional to x1.

At first glance, it might appear that Case 2 in Table 3.4 is quite similar to Case 1. However, Case 2 actually arises in a very different way. There no longer is a start-up cost, and the profit from the first unit of product 1 per week is indeed 3, as originally assumed. However, there now is an increasing marginal return; i.e., the slope of the profit function for product 1 (see the solid curve in Fig. 3.9) keeps increasing as x1 is increased. This vio- lation of proportionality might occur because of economies of scale that can sometimes be achieved at higher levels of production, e.g., through the use of more efficient high-volume machinery, longer production runs, quantity discounts for large purchases of raw materials, and the learning-curve effect whereby workers become more efficient as they gain experi- ence with a particular mode of production. As the incremental cost goes down, the incre- mental profit will go up (assuming constant marginal revenue).

Referring again to Table 3.4, the reverse of Case 2 is Case 3, where there is a decreasing marginal return. In this case, the slope of the profit function for product 1 (given by the solid curve in Fig. 3.10) keeps decreasing as x1 is increased. This violation of proportionality might occur because the marketing costs need to go up more than propor- tionally to attain increases in the level of sales. For example, it might be possible to sell product 1 at the rate of 1 per week (x1 = 1) with no advertising, whereas attaining sales to sustain a production rate of x1 = 2 might require a moderate amount of advertising, x1 = 3 might necessitate an extensive advertising campaign, and x1 = 4 might require also lower- ing the price.

All three cases are hypothetical examples of ways in which the proportionality assump- tion could be violated. What is the actual situation? The actual profit from producing prod- uct 1 (or any other product) is derived from the sales revenue minus various direct and indirect costs. Inevitably, some of these cost components are not strictly proportional to the production rate, perhaps for one of the reasons illustrated above. However, the real question

is whether, after all the components of profit have been accumulated, proportionality is a reasonable approximation for practical modeling purposes. For the Wyndor Glass Co. prob- lem, the OR team checked both the objective function and the functional constraints. The conclusion was that proportionality could indeed be assumed without serious distortion.

For other problems, what happens when the proportionality assumption does not hold even as a reasonable approximation? In most cases, this means you must use nonlinear programming instead (presented in Chap. 13). However, we do point out in Sec. 13.8 that a certain important kind of nonproportionality can still be handled by linear programming by reformulating the problem appropriately. Furthermore, if the assumption is violated only because of start-up costs, there is an extension of linear programming (mixed integer pro- gramming) that can be used, as discussed in Sec.12.3 (the fixed-charge problem).

Additivity

Although the proportionality assumption rules out exponents other than 1, it does not pro- hibit cross-product terms (terms involving the product of two or more variables). The addi- tivity assumption does rule out this latter possibility, as summarized below.

Additivity assumption: Every function in a linear programming model (whether the objective function or the function on the left-hand side of a functional con- straint) is the sum of the individual contributions of the respective activities.

To make this definition more concrete and clarify why we need to worry about this assumption, let us look at some examples. Table 3.5 shows some possible cases for the objective function for the Wyndor Glass Co. problem. In each case, the individual contri- butions from the products are just as assumed in Sec. 3.1, namely, 3x1 for product 1 and 5x2 for product 2. The difference lies in the last row, which gives the function value for Z when the two products are produced jointly. The additivity satisfied column shows the case where this function value is obtained simply by adding the first two rows (3 + 5 = 8), so that Z = 3x1 + 5x2 as previously assumed. By contrast, the next two columns show hypo- thetical cases where the additivity assumption would be violated (but not the proportional- ity assumption).

Referring to the Case 1 column of Table 3.5, this case corresponds to an objective function of Z = 3x1 + 5x2 + x1x2, so that Z = 3 + 5 + 1 = 9 for (x1, x2) = (1, 1), thereby violating the additivity assumption that Z = 3 + 5. (The proportionality assumption still is satisfied since after the value of one variable is fixed, the increment in Z from the other variable is proportional to the value of that variable.) This case would arise if the two products were complementary in some way that increases profit. For example, suppose that a major advertising campaign would be required to market either new product pro- duced by itself, but that the same single campaign can effectively promote both products if the decision is made to produce both. Because a major cost is saved for the second

product, their joint profit is somewhat more than the sum of their individual profits when each is produced by itself.

Case 2 in Table 3.5 also violates the additivity assumption because of the extra term in the corresponding objective function, Z = 3x1 + 5x2 - x1x2, so that Z = 3 + 5 - 1 = 7 for (x1, x2) = (1, 1). As the reverse of the first case, Case 2 would arise if the two products were competitive in some way that decreased their joint profit. For example, suppose that both products need to use the same machinery and equipment. If either product were pro- duced by itself, this machinery and equipment would be dedicated to this one use. How- ever, producing both products would require switching the production processes back and forth, with substantial time and cost involved in temporarily shutting down the pro- duction of one product and setting up for the other. Because of this major extra cost, their joint profit is somewhat less than the sum of their individual profits when each is produced by itself.

The same kinds of interaction between activities can affect the additivity of the con- straint functions. For example, consider the third functional constraint of the Wyndor Glass Co. problem: 3x1 + 2x2 < 18. (This is the only constraint involving both products.) This constraint concerns the production capacity of Plant 3, where 18 hours of production time per week is available for the two new products, and the function on the left-hand side (3x1 + 2x2) represents the number of hours of production time per week that would be used by these products. The additivity satisfied column of Table 3.6 shows this case as is, whereas the next two columns display cases where the function has an extra cross-product term that violates additivity. For all three columns, the individual contributions from the products toward using the capacity of Plant 3 are just as assumed previously, namely, 3x1 for product 1 and 2x2 for product 2, or 3(2) = 6 for x1 = 2 and 2(3) = 6 for x2 = 3. As was true for Table 3.5, the difference lies in the last row, which now gives the total function value for production time used when the two products are produced jointly.

For Case 3 (see Table 3.6), the production time used by the two products is given by the function 3x1 + 2x2 + 0.5x1x2, so the total function value is 6 + 6 + 3 = 15 when (x1, x2) = (2, 3), which violates the additivity assumption that the value is just 6 + 6 = 12. This case can arise in exactly the same way as described for Case 2 in Table 3.5; namely, extra time is wasted switching the production processes back and forth between the two products. The extra cross-product term (0.5x1x2) would give the production time wasted in this way. (Note that wasting time switching between products leads to a positive cross-product term here, where the total function is measuring production time used, whereas it led to a negative cross-product term for Case 2 because the total function there measures profit.)

For Case 4 in Table 3.6, the function for production time used is 3x1 + 2x2 - 0.1x2x , so the function value for (x1, x2) = (2, 3) is 6 + 6 - 1.2 = 10.8. This case could arise in the following way. As in Case 3, suppose that the two products require the same type of machin- ery and equipment. But suppose now that the time required to switch from one product to

the other would be relatively small. Because each product goes through a sequence of pro- duction operations, individual production facilities normally dedicated to that product would incur occasional idle periods. During these otherwise idle periods, these facilities can be used by the other product. Consequently, the total production time used (including idle periods) when the two products are produced jointly would be less than the sum of the production times used by the individual products when each is produced by itself.

After analyzing the possible kinds of interaction between the two products illustrated by these four cases, the OR team concluded that none played a major role in the actual Wyndor Glass Co. problem. Therefore, the additivity assumption was adopted as a reason- able approximation.

For other problems, if additivity is not a reasonable assumption, so that some of or all the mathematical functions of the model need to be nonlinear (because of the cross-product terms), you definitely enter the realm of nonlinear programming (Chap. 13).

Divisibility

Our next assumption concerns the values allowed for the decision variables.

Divisibility assumption: Decision variables in a linear programming model are allowed to have any values, including noninteger values, that satisfy the func- tional and nonnegativity constraints. Thus, these variables are not restricted to just integer values. Since each decision variable represents the level of some activity, it is being assumed that the activities can be run at fractional levels.

For the Wyndor Glass Co. problem, the decision variables represent production rates (the number of batches of a product produced per week). Since these production rates can have any fractional values within the feasible region, the divisibility assumption does hold.

In certain situations, the divisibility assumption does not hold because some of or all the decision variables must be restricted to integer values. Mathematical models with this restriction are called integer programming models, and they are discussed in Chap. 12.

Certainty

Our last assumption concerns the parameters of the model, namely, the coefficients in the objective function cj, the coefficients in the functional constraints aij, and the right-hand sides of the functional constraints bi.

Certainty assumption: The value assigned to each parameter of a linear program- ming model is assumed to be a known constant.

In real applications, the certainty assumption is seldom satisfied precisely. Linear pro- gramming models usually are formulated to select some future course of action. Therefore, the parameter values used would be based on a prediction of future conditions, which inevitably introduces some degree of uncertainty.

For this reason it is usually important to conduct sensitivity analysis after a solution is found that is optimal under the assumed parameter values. As discussed in Sec. 2.3, one purpose is to identify the sensitive parameters (those whose value cannot be changed with- out changing the optimal solution), since any later change in the value of a sensitive para- meter immediately signals a need to change the solution being used.

Sensitivity analysis plays an important role in the analysis of the Wyndor Glass Co. problem, as you will see in Sec. 7.2. However, it is necessary to acquire some more back- ground before we finish that story.

Occasionally, the degree of uncertainty in the parameters is too great to be amenable to sensitivity analysis alone. Sections 7.4-7.6 describe other ways of dealing with linear pro- gramming under uncertainty.

The Assumptions in Perspective

We emphasized in Sec. 2.2 that a mathematical model is intended to be only an idealized representation of the real problem. Approximations and simplifying assumptions generally are required in order for the model to be tractable. Adding too much detail and precision can make the model too unwieldy for useful analysis of the problem. All that is really needed is that there be a reasonably high correlation between the prediction of the model and what would actually happen in the real problem.

This advice certainly is applicable to linear programming. It is very common in real applications of linear programming that almost none of the four assumptions hold com- pletely. Except perhaps for the divisibility assumption, minor disparities are to be expected. This is especially true for the certainty assumption, so sensitivity analysis normally is a must to compensate for the violation of this assumption.

However, it is important for the OR team to examine the four assumptions for the problem under study and to analyze just how large the disparities are. If any of the assump- tions are violated in a major way, then a number of useful alternative models are available, as presented in later chapters of the book. A disadvantage of these other models is that the algorithms available for solving them are not nearly as powerful as those for linear pro- gramming, but this gap has been closing in some cases. For some applications, the power- ful linear programming approach is used for the initial analysis, and then a more complicated model is used to refine this analysis.

As you work through the examples in Sec. 3.4, you will find it good practice to ana- lyze how well each of the four assumptions of linear programming applies.